Micropitting is a type of surface damage that occurs in concentrated, rolling-sliding contacts, such as those between gear teeth, through rolling contact fatigue mechanisms. It differs from macropitting in that the damage initiates on the surface asperity level rather than the macro contact level. As such, micropitting is prevalent in contacts operating under low specific film thicknesses (Λ-ratios) and mixed lubrication regime, typical of gear teeth contacts. Micropitting is most commonly reported in gear teeth contacts, which typically operate at relatively low specific film thicknesses, but with the increasing use of less viscous lubricants, it has also been observed in rolling element bearings. Review of literature reveals multiple factors of influence in the onset and progression of micropitting in rolling-sliding non-conformal contacts. The relationship between the Λ-ratio and micropitting extent has perhaps received the most attention in the literature, and it is relatively well-established now that micropitting will only occur if the prevalent film thickness is low enough so that significant asperity-to-asperity contact occurs. For example, Olver and co-authors [1, 2] obtained micropitting damage in a triple disc rig only at Λ-ratios less than 0.12 and observed no micropitting at all with Λ-ratios over 0.16 (quoted Λ-ratios were based on Ra roughness values). Other effects, including contact pressure, material, and the magnitude and direction of sliding, have also been shown to have a significant influence on micropitting by several authors [3, 4]. Research also suggests that lubricant additives, including ZDDP anti-wear additives and friction modifiers, can promote micropitting by their effects on wear-in of surfaces and contact friction forces [2].
Recently, a parameter, referred to as SGF,Y, based on the extent of sliding, has been proposed as a potential criterion for the prediction of micropitting onset, as described in the Technical Report, ISO/TR 15144-1 [5], with the proposed reasoning being that the increased slide-roll ratio results in a lower local film thickness, hence promoting micropitting [5, 6]. However, as evident in the ongoing discussions in relations to the aforementioned proposal, the effects of slide-roll ratio on micropitting, and in particular the relevant mechanisms, are not well understood and require further clarification. Despite the fact that it is one of the major modes of gear failure, there are as yet no universally accepted design guidelines for prevention of micropitting.
This paper attempts to provide further insight into the influence of sliding on the extent of micropitting. Experimental results obtained under closely controlled contact conditions are presented, and further analysis and discussion are provided in an attempt to elucidate the mechanisms by which slide-roll ratio may promote micropitting. In particular, in light of this discussion, an effort is made to isolate the influences of film thickness from those of the slide-roll ratio in an attempt to provide a contribution to the ongoing discussions about suitable micropitting criteria.
Experimental Methods and Materials
Occurrence of micropitting in gear teeth contacts is often studied using component level tests — FZG back-to-back rig being perhaps the most common example. Although such rigs may be useful in ranking different lubricants in terms of their resistance to micropitting in gears, they do not allow for a systematic study of the influence of various contact parameters on the occurrence of micropitting because they do not provide independent control of the relevant contact variables, in particular coefficient of friction, specific film thickness, temperature, and slide-roll ratio. Furthermore, given that micropitting damage is caused by underlying rolling contact fatigue mechanisms requiring damage accumulation, crack initiation, and subsequent propagation, micropitting tests invariably take a long time.
The Micropitting Rig (MPR)
To overcome these problems, the present study uses a three-disc type rolling contact fatigue test rig, illustrated in Figure 1. The rig is produced by PCS Instruments and is often referred to as the MPR, or the micropitting rig. The test specimen is the central roller, which is in contact with three counterface discs (see Figure 2). Owing to the triple-contact configuration, the rig is able to generate more than 1 million contact cycles an hour in the test roller, while controlling all relevant contact parameters as described in this section.


Lubrication is achieved through a dip lubrication system with the counterface discs being partially submerged and dragging oil into all three contacts during operation. The lubricant sump is temperature-controlled. Heating is provided by a cartridge heater built into the test chamber casing, allowing for oil sump temperatures of up to 135°C. In addition, heat exchanger channels run through the base of the oil sump so that cooling or heating can be provided using an external unit as required. Lubricant temperature is measured using two RTD thermometers: one of them measures the temperature at the oil sump, and the other is positioned near the test specimen, providing a temperature measurement near the contacting surface of the roller specimen.
The roller and counterface discs are driven by two independent motors so that any slide-roll ratio in the range 0 to 200 percent can be achieved. The roller specimen shaft is equipped with a torque meter that provides a continuous measurement of torque throughout the tests, thus enabling the average contact friction coefficient to be monitored. This is helpful in any rolling contact fatigue study as it allows for monitoring of any changes in the lubrication regime over the test duration.

The maximum achievable entrainment speed with standard specimens and pure rolling is 4 m/s. The load is applied through the top counterface ring using a stepper motor and a loading arm, as illustrated schematically in Figure 3. The top shaft is supported by a floating bearing housing suspended on a strain-gauged loading arm. The loading arm is connected to a ball screw, which is driven by a stepper motor. As the ball screw is wound up by the motor, the top shaft bearing housing rotates around a pivot bearing so that the top counterface disc loads the roller specimen, and then the load is transmitted to the lower two roller-disc contacts. The three counterface discs are spaced 120° apart, which gives equal normal reaction forces at the three contact points with the central roller. The system allows the load to be controlled in the range of 0 to 2,000 N. Depending on the exact profile of the employed specimens and the resulting contact geometry, the maximum achievable contact pressure is in the range of 4.8 GPa.
It should be noted that the rig can be used to reproduce both micropitting and pitting failure modes. Indeed, Olver and co-authors employed the same rig in their studies of micropitting wear [1, 2].
Test Specimens
The specimens used in this study are a 12-mm-diameter cylindrical test roller and crowned discs where the crown radius transverse to rolling direction is 80 mm and the disc diameter in the rolling direction is 54.15 mm, as illustrated in Figure 4. Given the known influence of surface roughness on micropitting, the finish of the specimens was carefully controlled to minimize the variation from test to test as much as possible. All surface roughness values were measured using a stylus profilometer, and the quoted values are an average of four measurements for each specimen. Fresh rollers and discs had an average nominal root mean square roughness, Rq = 0.20 ±0.04 mm and Rq = 0.42 ±0.006 mm, respectively. It should be noted that the variation of the roller roughness is largely irrelevant since the roller is softer than the discs and its initial roughness is quickly modified in each test due to micropitting wear. In contrast, the roughness of the harder counterface rings is of major significance, and even small variations can affect the rate of micropitting. Although care was taken to ensure consistency of the counterface discs roughness, it should be said that some roughness differences between tests may still exist, however minimal. Due to the employed finishing process, all surfaces have circumferential roughness, i.e., lay is orientated in the rolling direction. It should be noted that the gear surface roughness is commonly orientated in the transverse direction, but the effects of roughness orientation are beyond the scope of this study. All specimens were made of case carburized 16MnCr5 gear steel with nominal composition shown in Table 1, and the test roller case depth of approximately 0.9 mm.


All tests were conducted with base PAO oil, which had 1.2% ZDDP (0.1%P) anti-wear additive added to it. This choice of non-commercial model oil was deliberate in order to closely control any influence of oil chemistry and specifically avoid any unknown effects of the commercial additive packages. The viscosity and density of the test oil was measured using a Stabinger viscometer with measured viscosity and density, respectively, being 25 cSt, 0.8108 g/cm3 at 40°C and 5 cSt, 0.7732 g/cm3 at 100°C. Viscosities at other temperatures can then be calculated using the ASTM D341-722 standard equation. It should be noted that the combined choice of oil, surface roughness, and temperatures in the present tests was made to ensure that the specific film thicknesses (as defined later) are sufficiently low to cause micropitting so that the micropitting damage phenomenon can be studied. The oils used in typical gearbox applications are usually more viscous than this, but other operating conditions, not least the surface roughness, is such that similar lambda ratios as in the present tests may be reached, resulting in the relatively widespread occurrences of gear micropitting. In effect, the applicability of the tests to real gearbox applications is ensured by realistic specific film thicknesses (Λ-ratios), specimen materials, and loading-contact parameters of primary significance to the onset of micropitting.
Test Procedure
Prior to testing, the test specimens and fasteners were ultrasonically cleaned in toluene and isopropanol for 15 minutes and dried. The test chamber of the rig was cleaned using toluene followed by isopropanol and then dried. In order to remove all traces of lubricant from previous experiments, as well as cleaning solvents, a flushing step was performed with the test lubricant prior to running the actual tests.
All tests at different slide-roll ratios were conducted to the same number of 5.12 million macro-contact cycles seen by the test roller specimen. (See Table 2.) The tests were interrupted at intervals in order to inspect the test specimens. Inspection included measurement of the roughness of counterface discs in order to evaluate the change of roughness in time, measurement of surface profiles of the roller, and taking optical micrographs of the roller surface. Surface profiles were measured using a Taylor Hobson Talysurf stylus profilometer with a vertical resolution of about 10 nm. The loss of diameter was taken as the measure of micropitting severity on the test roller. This was determined as the average of 4 Talysurf measurements transverse to rolling direction. Figure 5 shows a typical wear profile and illustrates how the value of maximum micropitting wear depth is obtained from it.


Isolating the Influence of SRR from Potential Thermal Effects:
Given that the primary aim of this study is to evaluate potential effects of the slide-roll ratio (SRR) on the level of micropitting, the test procedure was designed to closely control all other parameters while only varying the slide-roll ratio. In particular, as described earlier, it has been suggested that the primary mechanism in which increased slide-roll ratio results in elevated levels of micropitting is through the associated increase in contact temperatures and consequent drop in oil film thickness and reduction in Λ-ratio. Although it is well known that lower Λ-ratios do result in increased levels of micropitting, the effects of slide-roll ratio on prevalent film thickness are less clear [7], particularly within the slide-roll ratio range of 0 to 50 percent experienced in typical gear teeth contacts. Therefore, in order to establish the effect of the slide-roll ratio, it is necessary to control the Λ-ratio between different tests so that its effects on micropitting are separated from those of increased SRR. In parallel, the potential effects of SRR on film thickness were studied separately, using an optical interferometry-based film thickness rig.
Higher slide-roll ratios result in a higher amount of heat going into the contacting bodies and clearly, will increase the in-contact temperature of the lubricant. However, the EHL film thickness is governed by the properties of the lubricant, particular viscosity, in the EHL inlet zone rather than properties within the contact, which of course govern the EHL traction behavior. Therefore, if the contact setup is such that the heat flowing into the two contacting bodies increases the inlet temperatures (tooth bulk temperature in gear teeth contacts), the film thickness will be affected too. Consequently, the experimental procedure is designed to compensate for any difference in contact inlet temperature at different slide-roll ratios. This was done by first predicting what the inlet temperature rise may be, using an analytical method (based on a measured friction coefficient) and then adjusting the oil sump temperature to compensate for this temperature rise, hence keeping the inlet temperature and resulting film thickness constant for all tests, i.e., isolating the effect of slide-roll ratio on micropitting. This section will outline the procedure used to predict the inlet contact temperature rise.
Figure 6 illustrates the different temperatures of relevance to EHL contacts, namely oil film temperature, Toil, in-contact surface flash temperatures, Tf1 and Tf2, bulk temperatures of the two surfaces, Tb1 and Tb2 (which may be different if the two surfaces have different speeds), and the inlet temperature, Tb. The situation presented is analogous to a gear tooth contact where Tb is the bulk temperature of the contacting teeth and is often estimated by either assuming that it is 20°C higher that the sump temperature (TA) or by using an approximate relationship suggested by AGMA [8], where Tb = TA + 0.56ΛTf, max, where ΛTf, max is the maximum flash temperature rise along the path of contact during one mesh cycle. The method presented here attempts to provide more accurate predictions.

In cases where film thickness is low enough for significant solid-to-solid contact to occur, as is the case in the present tests conducted, the temperature difference across the oil film can be ignored (i.e. ΛToil = 0) so that the contact temperature, Tc, can be set to the surface temperature of either of the bodies, which are now equal, i.e., Tc = Tb1 + ΛTf1 = Tb2 + ΛTf2.
The method used here is based on that proposed by Olver [9] and has been successfully used in the past to study gear lubrication and efficiency [10]. Here, only the application of the method to the three-disc MPR rig is outlined, and the reader is referred to the referenced publications for further detail and the application of the method to gear teeth contacts.
Frictional heat is generated in contact between the specimens and then conducted away into their surfaces. As a result, the bulk surface temperature Tb rises above ambient Ta, which in this case is the oil supply temperature, but is below the maximum transient average temperature in contact Tc. In order to calculate Tb, the heat partition between the roller and counterface discs is considered. It is assumed that a portion of heat α is conducted into the roller in each of the three contacts while the rest (1-α) enters the counterface disc. This can be represented by the thermal network shown in Figure 7.

The contact temperature, Tc, is equal for the roller and discs as previously described, so that the heat partition fraction, α, can be obtained via Equation 1:
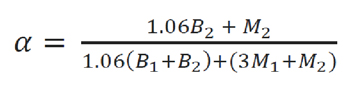 Equation 1
Equation 1
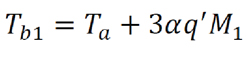 Equation 2
Equation 2
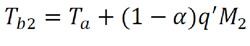
Equation 3
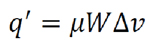 Equation 4
Equation 4
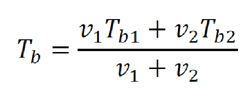 Equation 5
Equation 5
In the present study, the above analysis is applied to each set of test conditions used, and the value of oil sump temperature, Ta, changed so that the inlet temperature, Tb, and therefore the film thickness in each case, is the same in all tests. The exact test conditions used are outlined in the next section.
Test Conditions: The test conditions for the present study were chosen so that micropitting is reliably observed, while other modes of failure, particularly excessive wear and macropitting (spalling), were suppressed. Occurrence of wear (adhesive or abrasive), in particular, can make it difficult to study micropitting itself as it is a competing damage mechanism in that excessive surface wear usually prevents the onset, or progression, of micropitting itself. The two mechanisms are relatively easily distinguished by the appearance of the damaged surface, which, in the case of micropitting, clearly exhibits small, shallow micropits and short cracks, while an examination of the specimen sections parallel to rolling direction should reveal very shallow cracks, tens of microns in length at the most, inclined to the surface at an angle of around 30°. All results presented here show these classical features of micropitting as the dominant failure mode, although it should be noted that a very limited amount of wear may still be occurring in parallel, usually only in the early stage of the test, before the micropitting cracks develop. Based on previous tests conducted using the same equipment [1, 2], it was already known that micropitting is reliably observed at specific film thicknesses (Λ-ratios) of 0.16 and less. Furthermore, previous tests with similar materials also showed that contact pressures below 2 GPa are likely to result in micropitting, while higher pressures may cause macropitting. Based on this, the present study was conducted at a contact pressure of 1.78 GPa (500 N load on the rig) and entrainment speeds and oil sump temperatures that would produce Λ-ratio of about 0.10 in all tests (accounting for the bulk temperature rise as previously described). It should be noted that the quoted Λ-ratio is based on the counterface roughness only, i.e.:
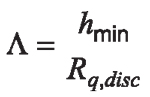 Equation 6
Equation 6
Three different slide-roll ratios were chosen for the preliminary study, namely 5%, 15%, and 30%. This range was deemed appropriate as it covers typical slide-roll ratios found in gear applications. Table 3 lists the complete set of conditions used in the present study.

Finally, given the rolling contact fatigue origins of micropitting, it was important to ensure that all tests were conducted with the same friction coefficient, regardless of the SRR. Given the previously described procedure to ensure the same Λ-ratio in all tests, so that effectively the experiments are conducted at the same point on the Stribeck curve, it was expected that the friction coefficient would indeed be similar for all tests. Inspection of the friction coefficient traces recorded by the MPR rig confirmed that the friction coefficient was the same for all tests, namely 0.09. This in turn provides some reassurance that the lubrication conditions (as described by the Λ-ratio, Equation 6) were indeed similar in all tests.
Results
Micropitting was observed in all tests listed in Table 3. Figure 8 shows example SEM images of micropitted roller surfaces at SRR = 5%, 15%, and 30%. It is evident that in all cases, surfaces contain numerous V-shaped cracks as well as small, shallow micropits (more clearly visible in sections illustrated in Figure 10) located between the individual cracks and producing a surface that is sometimes described as “peeled.” As previously discussed, these features are indicative of surface-initiated rolling contact fatigue mechanism ultimately responsible for micropitting. Figure 9 shows a close-up image of a somewhat larger micropit. In all cases, the micropits are formed by propagation of a V-shaped crack until a small, shallow segment of material (tens of microns across) detaches from the surface. The direction of friction force and the direction of contact motion are also indicated in Figure 8. It is evident that cracks grow against the direction of friction force. This crack growth behavior is broadly accepted as being typical of surface-initiated rolling contact fatigue cracks [13, 14], although the exact reasons for this relationship between initial crack direction and friction are not well understood. Entrainment of oil into the surface-breaking cracks and its subsequent pressurization by the over-rolling contact, resulting in the increase in the stress intensity factor at the crack tip [15, 16], is one mechanism that is commonly quoted to explain this apparent relationship. This seems entirely plausible given that the oil can only be pressurized if the contact approaches from crack mouth to crack tip, as has been postulated by various authors [15, 16].



Selected roller specimens were sectioned at the end of the test and sections polished for inspection to allow for closer inspection of morphology of the surface cracks leading to micropitting. Figure 10a shows a typical SEM image from one such section. It is apparent that the initial cracks grow into the surface at an angle and against the direction of friction force; behavior wholly typical of surface-initiated rolling contact fatigue. All observed cracks are relatively short — their length being in the order of tens of microns, which is typical of micropitting. Finally, Figure 10b shows a cross-section of a micropit formed by the propagation of a surface-breaking V-shaped crack.
As explained in the previous section, the progression of micropitting is measured by recording a surface profile across the roller wear track at specified intervals throughout the test. Figure 11 shows a series of such surface measurements at different test stages for the test with SRR = 5% illustrating the evolution of micropitting wear with the increasing number of test cycles. Plots for other tests show similar behavior but with different levels of micropitting wear at the equivalent test stages. From such plots, it is easy to obtain the maximum depth of the recorded wear track, and it seems reasonable to use this value as a measure of the level of micropitting at the given test stage. This in turn allows the level of micropitting to be plotted against the test cycles for each of the tests, thus allowing for easy comparison. Figure 12 presents such a plot for the tests at SRR = 5%, 15%, and 30%. It is immediately apparent that the increase in SRR increases the amount of micropitting wear, with the deepest wear track recorded for the SRR of 30% and smallest for SRR = 5%. Furthermore, the rate of micropitting wear (increase of wear depth per load cycle) is also the largest for SRR of 30% and smallest for SRR = 5%. Interestingly, it appears that, with current loading conditions, the incubation period for all three SRR is similar, as evident by the same amount of micropitting wear recorded for all three SRRs at the first test stage N = 90,000 contact cycles. However, this observation should not be generalized since differences in incubation period may well become apparent under other loading conditions.



Reasons for the observed increase in micropitting wear with increasing SRR will be considered in the next section. To aid this discussion, Figure 13 plots the measured micropitting wear at each test stage against the sliding distance achieved at the same stage, rather than the more usual number of cycles. The sliding distance is calculated as the product of sliding speed and test time. Clearly, given that the entrainment speed is set at 2 m/s in all tests, the higher the SRR, the higher the sliding speed and the resulting sliding distance for the given number of cycles. It is immediately apparent from this figure that micropitting wear rates for all SRRs fall more or less on the same curve, with any deviation within the acceptable variation in the experimental measurements. This strong relationship between the extent of micropitting and the sliding distance, regardless of the imposed SRR, clearly suggests that the mechanism by which increasing SRR increases the rate of micropitting is directly related to the distance by which the counterface discs slide over the slower test roller. The relevance of this is discussed in more depth later in the paper.
Discussion
The results presented in the previous section clearly suggest that there is a correlation between the slide-roll ratio and the severity of micropitting damage in rolling-sliding contacts. Namely, increasing the slide-roll ratio results in increased levels of micropitting wear. However, this trend was recorded despite the fact that the film thickness, and resulting Λ-ratio, was held constant in all tests, suggesting that the primary mechanism by which the increased level of sliding increases the amount of micropitting is not due to any film thickness effects. Furthermore, friction force, and hence tangential contact stresses, were also constant in all cases so that any influence of higher sliding (at least at these relatively high SRRs) is also not the primary cause of the increased micropitting. Consequently, it would be misleading to attempt to devise a design parameter to assess micropitting based on the assumption that higher SRRs reduce the EHL film thickness through the increase of in-contact temperature, as has been postulated in [5] and [6]. This follows from the fact that, although higher SRRs would indeed result in higher in-contact temperatures, it is the lubricant properties in the inlet of the contact that determine the film thickness, and the temperature in this region (inlet temperature) is generally not affected by slide-roll ratio, other than in cases of high levels of sliding where one component is near-stationary relative to the contact. In any case, the tests conducted in this study were designed to isolate the effects of SRR and film thickness through controlling the inlet oil temperature so that the two effects can be studied separately. In short, the obvious correlation between SRR and the severity of micropitting, combined with the well-established dependence of micropitting on the specific film thickness, does not in itself imply that the SRR and film thickness are correlated themselves.
Significant inlet heating can occur at very high levels of sliding but is unlikely to be significant at slide-roll ratios of 5 to 30% as used in this study. In isolated contacts, one would expect the film thickness to start dropping due to inlet heating only at very high slide-roll ratios. To confirm this experimentally with the oil used in the present study, film thickness measurements were conducted at varying SRRs and contact pressures using an optical interferometry rig. (See references [17] and [18] for further details of this well-established experimental technique.) The technique usually utilizes a ball-on-disc setup, but the contact geometry used in the current measurement was a barrel roller (radius ratio of 7:1) against a flat sapphire disc. This specimen geometry produces an elliptical contact with the major axis transverse to the direction of sliding and hence mimics relatively well the contact geometry used in the present micropitting tests so that any potential effects of this geometry are accounted for. The results are presented in Table 4. It is evident that the central film thickness remains unchanged as the SRR is increased from pure rolling to 50%, with a slight drop occurring at 100% sliding and a significant drop evident for pure sliding (SRR = 200%). These measurements confirm that a significant reduction in film thickness will only occur at very high levels of sliding in isolated contacts, as previously discussed.

In an attempt to provide an explanation for the observed increase in micropitting rates at higher slide-roll ratios and given that effects of film thickness and friction have been excluded as the possible explanations, the present study looked closer at rough surface contact mechanics conditions in the current tests. The analysis used a rough surface contact mechanics model originally devised by Cole and Sayles [19] and later extended by Kadiric et al [20] to predict contact pressures in the roller-disc contacts of the MPR test rig at the currently employed loading conditions. The analysis accounted for the measured rough surfaces of both components, and the calculations were done at different time steps during the contact passage so that the stress history of a given point (or an asperity) on the roller surface can be predicted. Figure 14 shows such stress histories for two random points on the roller surface during the contact passage at different SRRs as indicated in the legend. What is immediately apparent in these figures is that an increase in SRR results in an increased number of asperity stress cycles (micro-cycles). The curves for pure rolling (SRR = 0%) show a stress history that is representative of a smooth Hertzian contact, with an asperity experiencing one single stress cycle as it enters and leaves the contact, as may be expected. On the other hand, introduction of slide-roll ratio results in the same asperity sliding past a number of asperities on the counterface disc during its passage through the contact so that it now experiences a number of stress cycles. The higher the slide-roll ratio (for a fixed rolling speed), the more stress cycles the asperity will experience. This is apparent in the figure, particularly for higher slide-roll ratios of 30% and 90%, the latter deliberately included in this analysis to more clearly illustrate the described effect.

Given that micropitting is a rolling contact fatigue failure mode, clearly an increased number of stress cycles would result in increased severity of micropitting. Hence, the results of Figure 14 go some way in explaining the mechanisms by which the increased levels of sliding produce a higher amount of micropitting: higher slide-roll ratios simply increase the number of asperity stress cycles, which promotes contact fatigue on the asperity level and hence results in more micropitting. Indeed, this is supported by the fact that the micropitting progression plots for all SRRs collapse on the same curve when plotted against the sliding distance: the number of asperity contact cycles for a given surface roughness and entrainment speed is directly proportional to the sliding distance, and hence a given sliding distance, all else being equal, would be expected to result in the same amount of micropitting damage.
Conclusion
The study presented here describes a methodology to systematically study the influence of contact parameters on the occurrence and extent of micropitting in rolling-sliding non-conformal contacts with typical gear materials. The methodology utilizes a triple-contact rig where the contact pressure, entrainment speed, slide-roll ratio, and oil temperatures can be varied independently so that the effects of any single parameter can be isolated and assessed. This close control of influencing variables, combined with fast contact cycle accumulation, offers benefits over other ways of studying micropitting under conditions pertinent to gear teeth contacts. The presented results show that an increase in slide-roll ratio results in increased levels of micropitting but that the mechanism responsible for this observed increase is not a drop in film thickness at higher slide-roll ratios or an increase in friction coefficient, since both friction coefficient and film thickness were held constant in the current tests at all levels of sliding. Further analysis reveals that the mechanisms responsible for increased micropitting with increased sliding are related, at least in part, to the increase in the number of stress micro-cycles experienced by the surface asperities as the level of sliding increases. This is supported by the fact that the recorded micropitting rates for all levels of sliding tested here collapse on the same curve when plotted against sliding distance, which is directly proportional to the number of stress micro-cycles experienced by the asperities.
Therefore, it would seem that any potential design parameter devised to describe the effect of slide-roll ratio on micropitting should not be based on the effects of slide-roll ratio on in-contact temperature considerations as recently proposed, but should instead attempt to account for the increase in stress micro-cycles with increased sliding.
References
- Benyajati, C., Olver, A.V., Hamer, C. An experimental study of micropitting, using a new miniature test-rig. Tribology Series. 2003; 43: 601-10.
- Lainé, E., Olver, A.V., Beveridge, T.A. Effect of lubricants on micropitting and wear. Tribology International. 2008; 41(11): 1049-55.
- Webster, M.N., Norbart, C.J.J. An Experimental Investigation of Micropitting Using a Roller Disk Machine. Tribology Transactions. 1995; 38(4).
- Oila, A., Bull, S.J. “Assessment of the factors influencing micropitting in rolling/sliding contacts.” Wear. 2005; 258(10): 1510-1524.
- ISO/TR 15144-1, Calculation of micropitting load capacity of cylindrical spur and helical gears – Part 1: Introduction and basic principles. Second edition 2012-12-20.
- Elstorpff, M-G., Einflusse auf die Grubchentragfahigkeit ennsatzgeharterer Sahnrader bis in das hochste Zeitfestigkeitsgebiet. Disseration Techniche Universitat Munchen, 1993.
- He, T., Dong, Z., Jiaxu, W. Simulation of Plasto-Elastohydrodynamic Lubrication (PEHL) with Rolling Behaviors on an Elastic-Plastic Surface. ASME J. Tribol. 2016; 138: 031503.
- American Gear Manufacturers Association (AGMA); Preliminary information AGMA 925-A03 (1999).
- Olver, A.V. Testing transmission lubricants: the importance of thermal response. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering. 1991; 205(17): 35-44.
- Kadiric, A., Christodoulias, A., Olver, A.V., Sworski, A.E., Kolekar, A., Lockwood, F.E. The Efficiency of a Simper Spur Gearbox – Thermally Coupled Lubrication Model. AGMA Technical Paper. 14FTM08; 2014: 81-98.
- Jaeger, J. Moving Sources of Heat and the Temperature of Sliding Contacts. Journal and proceedings of the Royal Society of New South Wales. 1942; 76: 203-24.
- Hamrock, B.J., Dowson, D. Ball Bearing Lubrication: Elastohydrodynamics of Elliptical Contacts. 1981.
- Way, S. Pitting due to rolling contact. Journal of Applied Mechanics. 1935; 57: 49-58.
- Olver, A.V. The mechanism of rolling contact fatigue: an update. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology. 2005; 219(5): 313-30.
- Murakami, Y., Kaneta, M., Yatsuzuka, H. Analysis of Surface Crack Propagation in Lubricated Rolling Contact. ASLE Transactions. 1985; 28(1): 60-8.
- Bower, A.F. The Influence of Crack Face Friction and Trapped Fluid on Surface Initiated Rolling Contact Fatigue Cracks. Journal of Tribology. 1988; 110(4): 704-11.
- Cann, P.M., Spikes, H.A., Hutchinson, J. The development of a spacer layer imaging method (SLIM) for mapping elastohydrodynamic contacts. Tribology Transactions. 1996; 39(4): 915-921.
- < http://pcs-instruments.com/product/ehd-elasto-hydrodynamic-lubriction-2/ >.
- Cole, S.J., Sayles, R.S. A Numerical Model for the Contact of Layered Elastic Bodies With Real Rough Surfaces. ASME. J. Tribol. 1992; 114(2): 334-340.
- Kadiric, A., Sayles, R.S., Ioannides, E. Thermo-Mechanical Model for Moving Layered Rough Surface Contacts. ASME J. Tribol. 2008; 130(1): 011016-011016-15.
Printed with permission of the copyright holder, the American Gear Manufacturers Association, 1001 N. Fairfax Street, Suite 500, Alexandria, Virginia 22314. Statements presented in this paper are those of the authors and may not represent the position or opinion of the American Gear Manufacturers Association (AGMA). This paper was presented October 2016 at the AGMA Fall Technical Meeting in Pittsburgh, Pennsylvania. 16FTM21





































