Gear mesh misalignment may result in shifts in the load distribution of a gear pair that results in increasing contact and bending stresses, moving the peak bending stresses to the edge of the face width, and might also increase gear noise. This paper will discuss the sources of misalignment and show some examples of how this misalignment affects load distribution. Analyses will show how lead crowning and/or end relief can reduce the harmful effects of misalignment and then will discuss some of the pitfalls in the use of contact patterns to evaluate load distribution.
Example Gear Pair
Throughout this paper, the helical gear pairs defined in Table 1 will be used as examples. These gear pairs were part of a large test program of the Army and NASA [1] and have subsequently been analyzed and tested at The Ohio State University [2]. Figure 1 shows the transverse view of the helical gear pair with the superimposed line of action that is tangent to the base circles of the respective gears. Figure 2 shows a schematic of this line of action and also defines the coordinate systems to be used in this paper. Figure 2 shows how this line of action extends to a plane of action that now shows the superimposed diagonal lines of contact for one contact position. This plane of action is bounded on the top and bottom by the respective outside diameters of the two gears and on the edges by the face widths. The diagram would indicate that, for this position, there are three pairs of teeth in contact. Since the contact ratio is 2.63 at other positions, there will be two pairs of teeth in contact.



All simulation results presented in this paper will use a program entitled Load Distribution Program (LDP) that starts with the input geometry, discretizes the contact lines, and then simultaneously solves torque equilibrium and motion continuity equations [3-4]. Essentially the analysis of this program may be thought of as a special-purpose finite element solution that has many analytical simplifications that allow extremely time-efficient solutions.
Mesh Misalignment Definitions
In the gear contact sense, mesh misalignment implies the axial shifting of the position of the meshing surfaces due to either deflections or errors in the manufacture of the gears and their housings. The occurrence of any of these actions typically alters the location of contact on the tooth flank and may lead to large stresses and increased noise of a gear pair. Mesh misalignment may be divided into three categories:
1) Parallel misalignment (center distance change)
2) Angular misalignment parallel to the plane of action (MLOA)
3) Angular misalignment perpendicular to the plane of action (MOLOA)
Parallel misalignment, whether along the plane of action or at right angles to the plane, essentially results in a change in center distance of the shafts. A change in center distance will result in a slight change in the intersection of the outside diameters with the plane, thus slightly altering the profile contact ratio of the gear pair. Figure 3 shows this result for a contracting of the center distance, where a slight extension of the active contact area occurs, thus resulting in a slight increase of the profile contact ratio. For our gear pair, a contraction of 0.0002 inches results in the profile contact ratio shifting from 1.383 to 1.385, so this change is quite small and may usually be neglected in predictive analysis.

Unlike parallel misalignment, the effect of angular misalignment depends upon the plane that it acts in. Angular misalignment parallel to the plane of action tends to shift the load to the side of the tooth by increasing the separation at one side of the tooth and reducing the separation at the other side of the tooth. In this case, the shape and area of the theoretical active contact plane remains the same as the ideal shape of Figure 2. Figure 4 shows how this type of misalignment changes the load distribution from the aligned case to a case where the line of action misalignment is 0.002 inches across the face width (0.0016 in/in). We see that the load shifts sharply to the left, but that each contact line still has contact over its entire length.

However, when the angular misalignment is at a right angle to the plane of action, the outside diameters of the respective gears rotate as shown in Figure 5 in such a manner that the shape of the contact zone becomes skewed and the contact area is reduced. This reduction in contact area results in a reduction of total contact ratio. If this misalignment is severe enough, the effect on the contact lines will be similar to what would happen if two cylinders are skewed, where the contact line will change to elliptical contact as shown in Figure 6. This same skewing will occur for the lines of contact of both spur and helical gears.


Conversion of Misalignments
There are many causes of misalignment; some of them directly cause line of action (LOA) or offline of action (OLOA) misalignment, and others cause misalignment in rather arbitrary directions. Figure 2 shows a set of coordinate systems in which the shafts are aligned vertically in an x-y horizontal/vertical coordinate system. The appropriate gear mesh misalignment system is shown by the LOA and OLOA directions.
The normal convention in defining shaft misalignments would be to use the horizontal or vertical coordinate system in which x-direction misalignments would define changes along the centerline that are often called parallelism errors, and y-direction misalignments are at right angles to the centerline and are often referred to as skew misalignment. We shall refer to these misalignments as Mx and My, respectively. We will also assume that these misalignments are given in normalized units of mm/mm in Metric units or in/in in English units. Using these non-dimensional units, the values will be the same whether we consider Metric or English units.
In order to compute the misalignments in the LOA and OLOA directions, we need to use the following formulas:
MLOA = MxSinφ + MyCosφ , and
MOLOA = MxCosφ + MySinφ
Using a pressure angle of 23.45 degrees, the equations become:
MLOA = 0.398Mx + 0.917My, and
MOLOA = 0.917Mx + 0.398My
With regard to line of action misalignment, one finds that the y-axis “skew” misalignment is far more important than the parallelism misalignment. If one is given the misalignments in angular units as Mx and My, respectively, then the respective normalized misalignments along the x and y directions would be:
Mx = Tanθx and
My = Tanθy
If the misalignments of a 23.45 degree pressure angle gear are 0.002 in/in in the x-direction and 0.001 in/in in the y-direction we get LOA and OLOA misalignments of:
MLOA = 0.398*0.002 + 0.917*0.001 = 0.00171 in/in
MOLOA= 0.917*0.002 + 0.398*0.001 = 0.00223 in/in
The angular misalignments in degrees are:
θLOA = Tan-1(0.00171) = 0.09798 degrees
θOLOA = Tan-1(0.00223) = 0.12777 degrees
Check for Offline Action Misalignment Significance
The theory of Hertz [Roark] will be applied to determine whether the major axis the ellipse length of Figure 6. If the ellipse diameter is less than the face width, then it should be factored into load distribution calculations. The equations for calculating the ellipse diameters are given as:
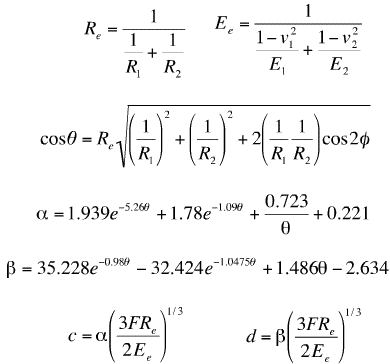

When the appropriate radii are inserted into the above equations, one gets the major radius to be about 15 in and the minor diameter is 0.007 in. The major diameter is obviously considerably larger than the face width of 1.25 in, hence the assumption of line contact of cylinders is upheld and there is no need to perform any special analyses. Even if the load is reduced by a factor of 10, the major diameter reduces to 5.5 in, which is still significantly larger than the face width.
Causes of Misalignment
Mesh slope and curvature misalignment of the gear mesh may result from many factors. The major ones are described as follows:
• Lead slope error. This error, which occurs when the gear teeth are cut, is described by the AGMA quality number and directly gives line of action misalignment.
• Lead wobble. This error in lead slope results from an angular eccentricity that occurs when mounting the gear. This occurs either when it is placed on its manufacturing arbor or when it is mounted to its shaft, and it wobbles relative to the shaft. Figure 7 shows sample lead charts for four teeth taken at 90-degree increments around a gear. The changing slopes of the four charts indicate lead wobble, and the average slope is the lead slope error listed above.

• Bore parallelism and skew. Here the error is most likely to be defined in terms of the x and y misalignments defined in the previous section. Often prints are very clear about the parallelism misalignment, but are sometimes a bit hazy with regard to the skew misalignment. Yet skew misalignment will have a greater effect on LOA mesh misalignment.
• Shaft bending deflections. For a single gear on a shaft, this deflection will be along the line of action, but when additional gears and other external forces are applied to the shaft, these deflections will take on a general direction. Also, for wide face width gears, this misalignment may have some curvature error as well as slope error. It is important to note that this misalignment is reasonably linear with load, so as load increases, the misalignment also increases .
• Shaft torsional deflections. In gears with wide face widths and low numbers of teeth, the twisting of the shaft due to the transmitted torque gives a helix angle or lead error.
• Bearing and housing deflections. Since both of these deflections are at the shaft support, they may be added together. Bearing stiffness increases with load, so the increase in bearing deflection with load is not directly proportional. As with shaft deflections, bearing deflections are in the line of action direction if only a single gear is mounted on the shaft, but are more general when additional forces are applied to the shaft. Housing deflections, which can exceed those of the bearings, are usually quite linear with load, but may need to be measured or need a detailed finite element analysis in order to be determined with some certainty. One should also be aware that the stiffnesses at the bearing has five degrees of freedom; three in translation, and two in rotation. Thus, to account for them properly, a complete bearing stiffness matrix must be determined.
• Gear blank deflections. The blanks of gears with thin rims tend to deflect away from the line of action on the overhanging section of the gear tooth. This deflection will tend to reduce the load carried in this region of the tooth.
• Spline and bearing clearances. Clearances that exist in mounting either the gear or the bearing will result in a tilting of the part in the line of action direction.
• Temperature gradients. These gradients are particularly apparent in helical gears, where the lubricant tends to be pushed along the helix and heats up as it progresses. The blank then heats up and expands, thus giving an apparent change in helix angle, as well as a slight change in all gear geometry parameters due to thermal expansion.
• Centrifugal forces. In thin-rim gears that spin at high speed, the centrifugal forces may be great enough to cause a differential deflection across the tooth face width, hence creating a form of misalignment.
Fortunately for the gear designer, the values of many of these misalignments are quite small for their application, but they each should be investigated to be sure that they do not impact a given design.
Center Distance Shifts
Center distance shifts may occur due to several factors:
• Bore parallelism error. This error, which may be obtained from the housing engineering drawing, might cause either a contraction or extension of the housing center distance.
• Shaft, bearing, and housing deflections. These deflections will usually cause an increase in the center distance.
• Mounted gear runout. Mounted runout includes the effect of manufactured eccentricity as well as mounting eccentricity. These eccentricities have the effect of increasing and then decreasing the effective shaft center distance at a period of one shaft rotation per each gear.
• Housing thermal expansion. This has the effect of increasing the center distance, but one must remember that the gear elements and shafts might also expand. If they are made of different materials, differential expansions must be considered.
• Clearance deflections. The mean deflection due to shaft and bearing clearances will add to the center distance change.
Calculation of Misalignment Effects
When considering misalignment, one must take into account the quality level of the gears, tolerances placed on engineering drawings, and deflections due to load or temperature. Misalignments related to tolerances or accuracy are assumed to occur in a random fashion, while those due to load or temperature may be much more systematic. In the latter case, it may be possible to provide mean changes to the lead to compensate for these effects. However, in so doing, one should be reminded that these systematic changes in alignment change with load, so any lead change will be good only at that load.
In the example calculation, AGMA Q9 (old definition) lead tolerances will be used for each gear (this translates to roughly an AGMA A8 gear using the new definition), a bore tolerance of 0.005 inch will be applied in the x and y directions, and the simple shaft model of the Load Distribution Program will be used to analyze shaft deflections. The gear set will be mounted on the shafting that is configured in Figure 8, where the shaft diameters are 1 inch and the bearing radial stiffness is 1e6 lb/in. We shall also assume that the temperature of the left side is elevated 150ºF and the right side is elevated 100ºF.

Figure 9 shows the shaft deflection and bearing deflection results of the LDP model when using a unit load (1.0 lb-in). The three different graphs indicate deflections if the mean load is placed at three different locations across the face width. In this case we shall assume the load is centered, so the middle trace will be used.

Mean Center Distance Variation
We shall first calculate the mean center distance factors that were discussed earlier. The transverse line of action tooth force of 2857 lb is used for all of the tooth deflection calculations.
• Bore parallelism error. The mean will be zero, but extremes due to tolerance will either increase or decrease the center distance by as much as 0.001 in (sum of the two worst case tolerances).
• Shaft, bearing, and housing deflections. The data from the center of the teeth in Figure 9 is used. Since the data is for the line of action, it must be converted to center distance coordinates using the sine function and the values must be doubled since the identical shafts will have the same deflections.
DELC1 = 2857*2(4.0+6.3)e-7sin(23.45°) = 0.00234 in
Mounted gear runout. Like bore parallelism, runout has a mean of zero, but will have minimum and maximum values that must be added for the two gears to get the maximum extremes. The AGMA Q9 runout is 0.002 in per-gear. Since this is a peak-to-peak value, one would expect the plus or minus values to be 0.001 in per-gear with the changes in center distance being twice this value or 0.002 in (two gears doubles the error).
• Housing thermal expansion. Multiply center distance by thermal expansion coefficient of steel and temperature change.
Left side: 150*6.8e-6*3.5 = 0.00357 in
Right side: 100*6.8e-6*3.5 = 0.00238 in
Deflection at the center of the gear = 0.00298 in (in the y-direction).
• Clearance deflections. These are unknown and will be assumed to be zero.
The final center distance change will have ±0.003 in (0.001 + 0.002) of random error and +0.00532 in giving a center distance range of: 0.00532 ± 0.003 in. Using the maximum center distance increase of 0.00832 in gives a reduction in the profile contact ratio of the gear pair from 1.383 to 1.328, and the backlash increases from 0.006 in to 0.0138 in.
Misalignment Slope at 4000 in-lb
Again, both random and systematic errors exist. Values will be calculated in normalized units of in./in, but may easily be converted to inches across the face width by multiplying by the face width of 1.25 in.
• Lead slope error.The AGMA Q9 lead error is 0.00048 in. Since this is the total span of the error, we shall divide it by two so that it gives the plus minus error of 0.00024 in. We must multiply this by two to take into account the possibility of both gears having maximum lead error at the same time and divide by the face width to get its value in normalized form. This random error then becomes:
MLOA1 = ±2*0.00024/1.25 = ±0.000384 in/in.
• Lead wobble. Mean is zero, so assume maximum and minimum to be the same as lead slope error:
MLOA2 = 0 ± 0.000384 in/in
• Bore parallelism and skew. Here we are going to assume that the tolerance on the bore locations in both the x and y directions are the same, so the tolerance of the bores along the line of action will be the same as the bore misalignment. This will be a random error that must be divided by the distance between the bearings to give a normalized value:
MLOA3 = 2*0.0005/4.75 = 0 ±0.000211 in/in
• Shaft bending deflections. Taken from Figure 9 and doubling for two shafts we get
MLOA4 = -2*2857*4.0e-7 = -0.001760 in/in
• Shaft torsional deflections. Taken from LDP we get which is nearly negligible.
MLOA5 = (2*2857*(0.12+0.08)e-7)/1.25 = 0.000091 in
• Bearing and housing deflections. From Figure 9,
MLOA6 = 2*2857*6.3e-7 = 0.0006 in/in
• Gear blank deflections. We are assuming a solid gear blank, so this is taken to be zero.
• Spline and bearing clearances. Again, taken to be zero.
• Temperature gradients. There is a 50-degree differential in temperature between the two bearings, with the left side bearing deflecting the most:
MLOA9 = -0.0012/4.75 = -0.000253 in/in
• Centrifugal forces. There is a 50-degree differential in temperature between the two bearings, with the left side bearing deflecting the most:
Total random misalignment: 0.000979 in/in
Total systematic misalignment: 0.001461 in/in
Range of misalignments = 0. 001461 ±0.000979 in/in
Here one could correct for the systematic error by putting a slope deviation of 0. 001461 in/in on the engineering drawing of the part, or one could treat this value as random misalignment in which case the worst-case misalignment would be 0. 000979 in/in. In the subsequent analyses we will assume the latter, and apply a worst-case misalignment of 0.002 in.
• Angular OLOA misalignment: Could be calculated, but for now assume to be ½ of the LOA misalignment = 0.15 degrees. This is very similar to the earlier calculation that concluded that the cylindrical contact used in the LDP calculation is extremely adequate.
Fortunately for the gear designer, the values of many of these misalignments are quite small for their application, but they each should be investigated to be sure that they do not impact a given design.
LDP Analysis of the Perfect Involute and Profile Modified Helical Gear Pairs
In addition to the load distributions of Figure 4, LDP also allows one to evaluate the contact stresses, transmission error, root stresses, and many other design evaluation parameters. Figure 10 shows the contact stresses for both the aligned and misaligned perfect involute helical gears whose load distribution is shown in Figure 4.

Table 2 summarizes the contact stress levels at several locations in the contact region. At both the entering and leaving corners of tooth contact, the stress levels get extremely exaggerated due to what is called corner contact [6]. This corner contact may be harmful or may simply get polished out so that the stress reduces closely to the surrounding values. If one wishes to eliminate this corner effect, the application of tip relief (removal of material at the tips of the teeth) is required. One notes that when the tooth pair is misaligned, the contact still covers most of the face width, yet the values of contact stresses that exclude the corners increase from 157 ksi to 242 ksi.

Selection of Optimum Lead Modification for the Helical Gear Pair
In order to compensate for misalignment, one often uses lead crowning or end relief [7] so that the loads and hence, stresses, do not rise at the tooth edges. We will next use the LDP program results to show the effects of both tip relief, circular lead crowning, and end relief on various gear design parameters. Selection of modification level and shape are such that transmission error — the main noise excitation — is minimized, while at the same time extreme levels of stresses and flash temperature are avoided for both the aligned and misaligned cases. Analysis is run at design load of 4000 lb-in.

Table 3 shows the results for four different cases of profile and lead modifications. Values in the table and their significance are given as follows:
• Corner contact: We have avoided quoting values for corner contact stresses, since they are estimates at best and, depending upon the simulation method, one can obtain a large range of values. However, the amount of corner contact is reported in a qualitative manner.
• Peak contact stress: The peak stress is recorded when 5 percent of the tooth face width and 5 percent of the tooth height is removed from the analysis.
• Root stresses: Gear1 and Gear2 root stresses are evaluated across the face width and the peak values are reported for each gear.
• Peak-to-peak transmission error: This is the motion error of the gears at the design load. Tip relief and lead crown were selected to minimize this parameter.
• Sum-of-forces [8]: This is a more complete noise metric that takes into account not only transmission error, but also friction forces and the axial shuttling of the mean tooth force that results from the movement of the contact lines across the tooth.
• Surface temperature: This is a metric that has been used to evaluate the sensitivity of a design to scoring and other surface damage. It accounts for contact stresses as well as sliding velocity in the contact region.
Four different micro-geometries are evaluated for the helical gear, and the summary is as follows:
1) Perfect involute (NoMod): Note that misalignment greatly increases most of the parameters.
2) Profile crown only (Case I): In order to minimize peak-to-peak transmission error of the aligned set, 0.0011 in a circular tip modification is applied. Note that tip relief alone results in a large reduction in the noise excitations and flash temperature, even when misaligned, but results in increases in both contact stresses and root stresses. These increases result because any removal of material tends to centrally focus the loads, hence increasing stresses.
3) Profile crown and lead crown (Case II). 0.0120 in of circular lead crown was applied to the tip relieved gear. Since we are further focusing the load, both contact stresses and root stresses of the aligned part increase further. However, the lead crown lowers stresses for the misaligned gears. It is interesting that the noise excitations increase, but are still less than those of the perfect involute.
4) Combinations of tip relief and lead relief (Case III). Here we apply end relief and a more complex shape of profile modification that is shown in Figure 11. The resulting contact stresses plot for the aligned and misaligned gear pair are shown in Figure 12.


Comment on Contact Patterns
Contact patterns are one of the only simple ways of identifying misalignment of a gear pair. However, contact patterns can be extremely deceiving for several major reasons:
1) The thickness of the dye tends to widen the pattern.
2) The pattern is an average of all of the meshi
3) The pattern says nothing about contact stress level within the pattern.
4) If one is running the gear pair at many loads, the pattern will exhibit the extreme summation of the pattern at each load.
In situation 2, for instance, if there is lead wobble in the mating part, the contact will move back and forth across the face width. The resulting contact pattern will superimpose each of the individual patterns, and the result will be that the measured pattern extends on both sides to the extremes of the individual patterns. Figure 10 illustrates this very well. The contact pattern for both the aligned and misaligned gears are shown in Figure 12.
Summary
Gear misalignment comes from a number of sources that have been identified in this article. Techniques such as lead crowning can assist the designer in minimizing the effects of misalignment, but requires some compromises by the designer. This paper has quantified some of the compromises that need to be made and has shown the value of load distribution analysis in assessing the effects of misalignment on key design parameters such as root and contact stresses, transmission error, and surface temperature.
References
- Drago, R., Lenski, J., Spencer, R., Valco, M., and Oswald, F.B., “The Relative Noise Levels of Parallel Axis Gear Sets with Various Contact Ratios and Gear Tooth Forms,” AGMA Fall Technical Conference. 1994.
- Houser, D.R., Drago, R.J., Oswald, F.B., Valco, M.J., “Comparison of Transmission Error Predictions with Noise Measurements for Several Spur and Helical Gears,” Proceedings of 30th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Indianapolis 1994.
- Conry, T., Seireg, A., “A Mathematical Programming Technique for the Evaluation of Load Distribution and Optimal Modifications for Gear Systems,” Journal of Engineering for Industry, Trans. ASME, Vol.95, No.4, Nov. 1973, 1115-1123.
- Houser, D.R. and Harianto, J., “Load Distribution Program Manual,” GearLab-The Ohio State University, 2002.
- Roark, R.J., “Formulas for Stress and Strain,” McGraw Hill, NY, 1965.
- Singh, A., and D.R. Houser., “Analysis of Off-Line of Action Contact at the Tips of Gear Teeth,” SAE Paper 941716.
- D.R. Houser, S. Chang and J. Harianto, “Tooth Flank Corrections of Wide Face Width Helical Gears that Account for Shaft Deflections,” DETC2003/PTG-48072, The American Society of Mechanical Engineers (ASME) and American Gear Manufacturing Association (AGMA), 2003 ASME/AGMA International Power Transmission and Gearing Conference, Chicago, IL, September 2003.
- D.R. Houser and J. Harianto, “Manufacturing Robustness Analysis of the Noise Excitation and Design of Alternative Gear Sets,” Proceedings of the 2001 Noise and Vibration Conference (2001-01-1417), SAE Technical





































