Rolling Contact Fatigue of Surface Densified PM Gears

Surface densification provides the opportunity for PM technology to advance into the manufacture of highly stressed product groups, such as automotive transmission gears. A key durability design requirement for such applications is the determination of allowable operating stresses for gear tooth rolling contact fatigue.

The paper shows that rolling contact fatigue performance is defined by the interaction of material shear fatigue strength and the applied subsurface shear stress profile. Appropriate selection of surface densification depth and heat treatment case depth provides PM gears with rolling contact fatigue durability which is at least equivalent to that of wrought steel. However, it is shown that some rolling contact fatigue test methods may underestimate the surface durability of surface densified PM materials.

Rolling contact fatigue test methods are reviewed with respect to failure modes, the microstructure of surface densified PM materials, and the gearing geometry of potential automotive transmission applications. Development of rolling contact fatigue test methods is recommended to enable the generation of test stress profiles that represent those which exist in actual gearing applications.

Introduction

Surface densification substantially improves the rolling contact fatigue and bending fatigue durability of PM components. The application of surface densification technology therefore provides opportunities for PM manufacturing to expand into highly stressed product groups such as gears, cams, and bearings [1-7].

The volume and precision manufacturing capabilities of the PM process, together with the enhanced durability provided by surface densification, has led to significant development effort with respect to automotive transmission gearing applications [8-12].

It has been shown that with surface densification, PM gears can be manufactured with surface durability and bending fatigue performance that is at least equivalent to wrought steel components [1,2,11,12]. A critical aspect in the achievement of such levels of mechanical performance is to ensure that component peak operating stresses are contained within the surface densified layers.

To characterize the surface durability of wrought steels, several types of rolling contact fatigue tests have historically been used. The progression has been to employ the same type of test methods in the evaluation of PM materials. The rolling contact fatigue tests are used to define allowable surface contact stress design data and to rank the performance of different materials and processes. Carburized grades of alloy wrought steels are usually used as a benchmark in those tests.

In this review it is shown that some of the previously used rolling contact fatigue test methods are not complementary with automotive transmission gear designs. In the analysis, gear tooth contact stresses and the generated subsurface stress profiles are related to the microstructure and to the fatigue strength profiles which exist in surface densified gears. The involute gear tooth forms of candidate automotive transmission gears are characterized to enable the definition of actual component operating stress conditions. It is shown that the geometry at the position of the contacting surfaces, specifically radius of curvature, can significantly influence the subsurface shear stress distribution. Rolling contact fatigue test methods are then reviewed in reference to gearing stresses and to the density profile of surface densified gears.

Gear Tooth Contact Stresses

Gear tooth involute surfaces move across each other with a combination of rolling and sliding actions. The tooth flank surface contact stress concentration that is introduced during the meshing of gears is illustrated in Figure 1a. The hertzian contact stresses that arise from the localized contact pressures can be analyzed from the perspective of two contacting cylinders which have radii that are representative of the curvature of the gear teeth involute surfaces [13,14], as shown in Figure 1a.

F is the applied force (N) to the cylinders of length L (mm) and of radii R (mm), with elastic constants, ν = poissons ratio, E = elastic modulus (GPa).

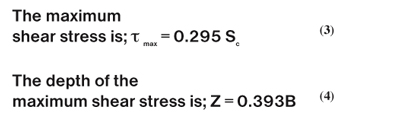
Subsurface Stress Distribution

The subsurface shear stress distribution that is induced by the contact condition may be determined using the principal stress equations shown below [15].

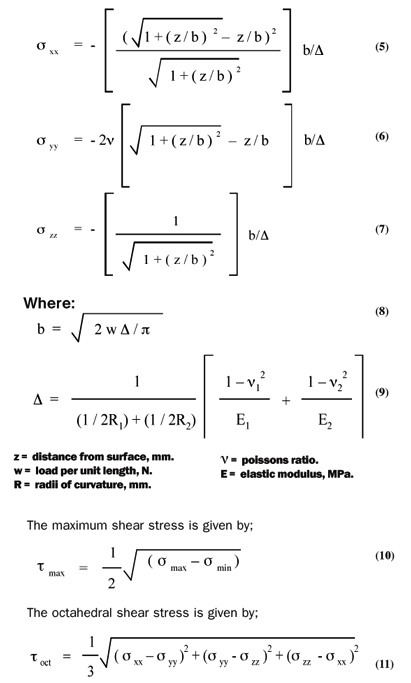
Using equations 5 to 11, taking radii of curvature, R1 = 6.1 mm, R2 = 15.1 mm, from an automatic transmission sun and pinion gear set (from Tables 1 and 3) with, E=207 GPa, ν = 0.3, and assuming a surface contact stress of 1800MPa (~ 260,000 psi), which is a typical upper level gear operating contact stress, the calculated subsurface stress profiles are shown in Figure 2.

In gear tooth cyclic loading conditions, the shear stress excursions shown in Figure 2 can lead to contact fatigue failures because of the repeatedly applied compressive stresses. The shear stress plots show that τ max is the higher maximum value, but it has been shown that the octahedral stress τoct is the most critical in defining allowable material operating stresses [15,16]. To provide durable component design in rolling contact fatigue applications, the applied shear stress profile must be adequately contained within the material strength capabilities. In gear applications, for wrought steels, the major considerations are case hardness profile and core hardness, for PM materials density gradient is an additional factor.

It is known that PM material elastic properties are a function of density [17,18]. The effect of density and hence the modified elastic properties on the subsurface shear stress profile are shown in Figure 3. The shear stress profile of the wrought steel curve from Figure 2 is compared with the stress profiles that arise with the application of PM material elastic properties.

At a given applied contact load, reduced density and the proportionally lower modulus allows greater surface deformation and hence broadening of the contact zone, so the peak shear stress is therefore reduced (7.86 g cm^-3 = 473 MPa, 7.5 g cm^-3 = 438 MPa, and 7.0 g cm^-3 = 394 MPa). In PM materials of uniform density, when evaluating near surface (<0.3 mm) stresses the appropriate lower density elastic constants must be selected. However, in consideration to surface densified materials, it is reasonable to assume the use of wrought steel elastic properties. In Figure 3, it is shown that at around 0.3 mm to 0.4mm, if the near surface (higher modulus) peak of curve (a) is positioned onto the lower modulus curve (c), the result is essentially the original curve of the fully dense material. Advanced microscopy or spectroscopy methods [19] to measure the contact zones within surface densified specimens would provide valuable insight into this aspect.

Surface Densified Gear Teeth

An example of a surface densified PM pinion for an automatic transmission is shown in Figure 4. Details of the tooth microstructure are shown in Figure 5: a section through the densified layer in 5a, the density profile measured by image analysis in 5b, and the case hardness profile 5c. The peak subsurface shear stresses shown previously in Figure 3 are contained within the surface densified layer. The layer of essentially fully dense material extends to a depth of around 0.3 mm with a gradient that intersects the core density of 7.5 g cm^-3 at a distance from the surface of approximately 1mm.

Rolling Contact Fatigue Failure Modes

Gear profile deterioration as a consequence of rolling contact stresses may occur either by pitting fatigue or by subcase fatigue failure modes [20]. The failure description terminology used in this paper follows the AGMA recommended nomenclature [21]. The subcase fatigue failure mode has been previously described by other terms, for example spalling and case crushing. The microstructural appearance of the failure modes has been differentiated as follows [22].

Pitting failure is characterized by relatively shallow fractures which are contained within the near surface case hardened region. The fracture path follows an acute angle relative to the gear flank surface, Figure 7.

Subcase fatigue failure shows deeper fracturing, usually at the case/core interface. The primary fracture path propagates parallel to the surface with secondary branches that are perpendicular to the surface and the primary case/core fracture, Figure 7.

The pitting fatigue stress limit is a material property defined by material and processing conditions. Subcase fatigue failure can be prevented by case depth selection; usually the minimum case depth that satisfies the subcase fatigue criterion is used. Excessive case depths are avoided in order to maximize bending fatigue durability [23]. Empirical case depth design guides for subcase fatigue in wrought steel gears have been developed and are shown by equations 12 and 13.

Where: ECD is the effective case depth to 50 HRC, Wt is the tangential load, lb, F is the gear face width, in, and φ is the pressure angle [24] (original reference units).

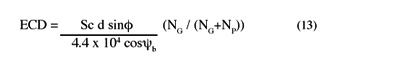
Where: ECD is the effective case depth to 50HRC; Sc is the maximum surface compressive stress, MPa; d is the pinion pitch diameter, mm; φ is the transverse pressure angle; ψb is the base helix angle, NG and NP are the number of gear and pinion teeth respectively [25].

Shear Stress and Shear Strength Profiles

Analytical design methods for the prevention of subcase fatigue failure have been proposed where case hardness profiles are converted to localized material strength profiles [22,26]. The earlier method based on localized yield strength values concluded that to avoid subcase fatigue failure the ratio of material shear yield strength to the applied shear stress must be greater than 1.8 [22]. The later method, based on calculated localized fatigue strength, concluded that the material shear fatigue strength should exceed the applied shear stress by a factor of 1.3 [26]. The latter procedure is preferred because of the use of fatigue strength factors rather than yield strength. However, in both studies it was demonstrated by gear tests that the developed criteria did prove to be successful in the prevention of subcase fatigue failure.

Figure 8 illustrates the interaction between the material shear strength and the applied shear stress profiles. The near surface high hardness material has adequate fatigue strength to contain the peak subsurface shear stress, and hence provide pitting fatigue resistance. Compressive residual stresses from carburizing heat treatment further assist in providing pitting durability. At the case/core interface (~0.9 mm in Figure 8) the proximity of the applied stress to the material fatigue strength indicates a probability of subcase fatigue failure. A deeper carburized case is required to increase the shear strength/shear stress factor to avoid subcase fatigue. With PM materials a deeper depth of surface densification may also be required. In subcase fatigue design the residual stress contribution is not a significant factor, since at the case-core interface region the magnitude of residual stress is usually small [22,27,28].

The material shear fatigue strength profile in surface densified materials can be estimated by the procedure developed for wrought steels [26], but modifications must be included to consider the density gradient. To establish the relation of hardness and density to tensile strength, test bars were manufactured through the density range of 7.0, 7.2 and 7.5 g cm^-3. Carbon increments of 0.2, 0.35, and 0.65 percents were selected to represent the carbon profile and hardness levels within carburized components. The base alloy content was constant with 0.9 percent Mn and 0.5 percent Mo. The test bars were sintered at 12800C, machined into tensile test bars, through hardened by oil quenching, and tempered at 1800C. Figure 9 shows the relation between particle hardness (HV0.1) and tensile strength. Comparative literature data is provided for wrought steels [29].

In reference to Figure 5, where gear hardness and density profiles are quantified, Figure 9 can be used to estimate equivalent local tensile strength (σ_u) at a given distance from the surface. Fatigue strength (σ_f) can then be estimated from tensile strength.

The previous work [26] used the accepted wrought steel fully reversed axial fatigue ratio (σ_f = 0.5 σ_u ). However, for PM materials it is known that the fatigue ratio is influenced by density, for example at 7.0 g cm^-3 an axial fatigue ratio of σ_f = 0.3 σ_u has been shown [18]. To estimate the local fatigue strength, a linear fatigue ratio change with density was assumed (from 0.3 at 7.0 g cm^-3 to 0.5 at 7.86 g cm^-3). The shear fatigue strength can be estimated from axial fatigue strength by the relation τ_f = σ_f /√3 [30]. The τ_f relation has been demonstrated for wrought steels, shear fatigue test data are needed for PM materials. However, since PM material shear yield strength values have been shown to follow the wrought steel relationship for tensile yield [18], it does appear to be reasonable to use the wrought steel shear fatigue relation in the comparative shear strength/shear stress profile approach for the PM materials.

The above methods of calculating local shear fatigue strength values were applied to the automatic transmission pinion example of Figure 4 and Figure 5. Together with the calculated shear stress profile of Figure 2, the resultant shear strength and shear stress plots are shown in Figure 10. It is clearly shown that the operating stresses are contained within the material fatigue strength capabilities. Additionally, the subcase fatigue criteria are shown to be satisfied, with a shear fatigue strength to shear stress ratio of 2.7 at the case/core interface distance of 1.0 mm. In this instance, performance was validated by four square gear rig durability tests where pitting fatigue was the observed failure mode.

An example of pitting in a surface densified layer is shown in Figure 11, and subcase fatigue failure due to an insufficient densified layer is shown in Figure 12. The differences in appearance of the failure modes are consistent with the wrought steel examples that were shown earlier (Figure 7).

Automotive Gears

Automotive transmission gear examples are shown in Figure 13 – 15. All of the gears are currently manufactured from carburizing grades of alloy steels, and the effective case depth after heat treatment is typically in the range of 0.5mm to 1.0mm.

The automatic transmission and front wheel drive manual transmission gears represent the highest volume gears and are most suited to manufacture by PM processes. The heavy duty rear wheel drive truck application is an example of the upper limit that is suited to PM manufacture; the overall gear size, requiring compaction press capacity of over 800 tons together with relatively lower production volume requirements, are limiting factors.

Key dimensions of the gear examples from the various applications are given in Table 1. The gearing data are used in the next section in the evaluation of gear tooth involute curvature, a critical consideration in rolling contact fatigue testing.

Involute Curvature

The involute gear tooth surface shows a change in radius of curvature when moving from the origin of the involute curve as shown in Figure 16. The radius of curvature, ρ, can be calculated as given by [13].

The calculated radii of curvature from equations 15 and 16 for the truck sun and pinion example of Table 1 are shown in Figure 17.

Pitting fractures usually initiate at a location just below the pitch diameter. The position corresponds with the point of minimum tooth deflection and minimum load sharing. Figure 18 illustrates the location as the 16 degree roll angle position for the particular straight spur gear under study. At roll angles of less than 16 degrees and greater than 26 degrees, tooth sharing reduces deflection and contact stress. Between 16 and 26 degrees, as the loading position moves toward the tip of the tooth, the tooth cantilever geometry allows increased tooth deflection, and hence reduced contact stresses [31,32].

Figure 19 illustrates the change in contact stress over the involute surface as a consequence of the tooth deflection characteristics. The contact stress increases toward the highest and lowest points of single tooth contact, the peak contact stress occurs at the LPSTC [20].

The transverse radii of curvature for the HPSTC and LPSTC positions can be calculated from equations 17 to 20 that are shown in Table 2 [33].

In consideration to the gear examples shown in Table 1 equations 14 to 20 give the radii of curvature shown in Table 3.

The worst-case pitting position occurs with contact at the pinion LPSTC and the gear HPSTC. The equivalent contacting cylinder diameters at the critical position are in the range of 11.4 mm to 30.2 mm for the high volume manufactured gears. The larger but lower volume gear has equivalent diameters of 15.8 mm to 56 mm. The established ranges of radii of curvature for the gear applications can be used as a reference for the stress conditions that are generated within rolling contact fatigue tests.

Rolling Contact Fatigue Testing

Various test geometries have been used to characterize rolling contact fatigue properties of wrought steels. Product groups of major interest are bearings, gears, cams, or railway components. The tests usually involve generation of contact stresses by the rotation of spherical or cylindrical elements under load [34-36].

Tests based on spheres can only provide comparative material ranking for gear applications. The stress pattern from spherical surface contact differs from that of cylindrical contact because of surface sliding effects shown in Figure 20 [37-39] and stressed material volume effects [40]. The result is that for a given test stress level, sphere and cylinder tests will show differing fatigue life results [41]. To provide surface durability data that can be used in gear design calculations, cylinder type test methods more closely represent the gear tooth line of contact and are therefore preferable. Test methods which have been applied to PM materials are summarized in Table 4.

Key parameters of the rolling contact fatigue test are:
• maximum contact stress,
• relative surface sliding,
• lubrication conditions,
• subsurface shear stress profile.

Maximum contact stresses of around 1700 MPa to 2000 MPa typically are used to determine fatigue limit data for wrought steels, hot forged PM, and surface densified PM materials. Higher test stress levels are used to establish the slope of the fatigue curve in the low cycle failure mode. Lower test stress levels are used to test non-surface densified PM materials since surface porosity significantly reduces rolling contact fatigue strength.

Test cylinder sliding is introduced to simulate the surface action which occurs during the meshing of gear teeth. To determine the appropriate range of sliding to use in cylinder tests, gear tooth surface sliding velocity can be determined from equations 21 to 25 (original reference units) [33].

Sliding values for the transmission gear examples of Table 1 are shown in Table 5. The amount of relative surface sliding is application dependent, a wide range of 3 to 15 percent is shown. The previously used rolling contact fatigue test methods have used sliding values of 24 to 43 percent.

Rolling contact fatigue durability is reduced in the presence of sliding forces because the magnitude of the surface shear stress is increased and the peak shear stress moves toward the surface, which eases fracture initiation [16,26,49]. Figure 21 shows data from through hardened roller bearing material tests where the introduction of the small amount of 3 percent sliding caused a significant reduction in fatigue strength of 22 percent; at greater levels of sliding of up to 20 percent a reduced proportional decrease in fatigue strength of around 14 percent was observed.

Comparative testing on wrought steel gears showed a maximum pitting frequency when the sliding ratio was between 3 and 10 percent [50]. More test results are required to establish the effect of sliding with surface densified PM materials, but with the test data that are available together with the shown calculated surface sliding values of the gear examples, a sliding component of less than 15 percent appears to be appropriate for rolling contact fatigue tests on surface densified PM gear materials.

Test lubrication conditions are usually established to create full film conditions where metal to metal contact is avoided, and elastohydrodynamic conditions are usually developed which can contribute to an increase in peak near surface contact stresses [19, 50]. It has been shown that surface densified PM materials behave in a similar manner to wrought steels in reaction to the elastohydrodynamic conditions.

Some test data have shown that the rolling contact fatigue limit of surface densified PM material may be slightly greater than that of the typically used gearing grades of wrought alloy steels [7,12,]. Contributing factors could be the combined influences of microstructure directionality and inclusion content [51,52]. More work is necessary to define these effects in further detail. The sliding and the elastohydrodynamic stress profile modifications are limited to the surface or near surface layers, so pitting fatigue performance therefore can be most significantly influenced. Since the deeper subsurface stress profile is not greatly affected, subcase fatigue failure is not significantly changed by the sliding and elastohydrodynamic conditions that occur in automotive transmission gear applications.

The subsurface shear stress profile is significantly influenced by the radius of curvature at the line of contact. Figure 22 shows the pinion and sun gear shear stress profile of Figure 2 compared to the calculated stress profiles for two of the cylinder based rolling contact fatigue tests of Table 4. In all three cases the application of a contact stress of 1800 MPa provides the same peak shear stress value of 473 MPa.

However, the increase in radius of curvature substantially changes the depth of the maximum stress from 0.11 mm to 0.24 mm and, further, to 0.4 mm. In reference to the pinion surface densified layer of Figure 5, it can be seen that rather than the peak stress being well contained within the surface densified layer, the cylinder tests would move the peak stress into the lower density region.

Also in reference to the subsurface material shear strength profile of Figure 10, due to the more deeply penetrating subsurface stress profile, the cylinder tests are likely to introduce subcase fatigue failure rather than the pitting that is observed on gears. The cylinder tests may therefore underestimate the pitting fatigue durability of surface densified materials.

Figure 23 illustrates the relative positions of the shear strength and the shear stress profiles. In the deeper case regions, the adverse interaction of the stress profiles from the larger radii cylinders, (b) and (c), with the shear strength curve, τ_f, is clearly shown. Test specimens can be processed to match the stress profiles that are introduced during the cylinder tests. The gear shear strength/shear stress profiles of Figure 10 can be factored to identify the density and case profiles which are needed for the cylinder test specimens.

However, to produce shear strength and shear stress profiles which are comparable to those in gears, the full density surface layer may need to be up to four times that which is usually applied to transmission gears. Similarly, to avoid subcase fatigue failure, densification and effective case depths of up to four times those usually used in gear manufacture will be needed. The resultant “deep case” material condition would not represent that which is usually used in automotive transmission gearing applications.

A preferable solution is to develop test methods which introduce stress profiles that are more representative of those in actual automotive gearing applications. Gear-like surface densified layers and heat treatments could then be evaluated, and such tests would also facilitate the determination of pitting performance in isolation from subcase failure conditions and hence provide more valuable design data. A potential test method is shown in Figure 24 [53].

Conclusion

Subsurface shear stress profiles and material shear fatigue strength profiles are shown to be defining design criteria with regard to rolling contact fatigue in surface densified PM gears. The shear stress and shear fatigue strength model can be used to specify microstructural conditions that are required to provide both pitting fatigue and subcase fatigue durability. Application of those parameters can provide surface densified PM gears with surface durability that is at least equivalent to that of wrought steel gears.

It is shown that further development of rolling contact fatigue test methods is required to provide pitting fatigue design data from cylinders that consist of surface densification and case depths that are representative of automotive transmission gears. The currently used tests, which are based on relatively large diameter cylinders, are likely to underestimate the surface durability of surface densified materials because of the introduction of subcase fatigue fracture, the failure mode that is usually removed in actual components by the shown case depth design considerations.

References

[1] P.K. Jones, K. Buckley-Golder, R. Lawcock, R. Shivanath, Densification Strategies for High Endurance PM Components, Int. J. Powder Metallurgy, v33, n3, p37-44, 1997.
[2] P. K. Jones, K. Buckley-Golder, D. Sarafinchan, Developing PM Gear Tooth and Bearing Surfaces for High Stress Applications, Int. J. Powder Metallurgy, v34, n1, p26-33, 1998.
[3] R. Lawcock, K. Buckley-Golder, D. Sarafinchan, Testing of High Endurance PM Steels for Automotive Transmission Gearing Components, SAE 1999-01-0293, Michigan, 1999.
[4] C. Cole, UK Patent GB 2,250,227B, 1994.
[5] P.K. Jones, K. Buckley-Golder, US Patent, 5,540,883, 1996.
[6] C. Cole, R. Shivanath, P.K. Jones, US Patent, 5,884,527, 1999.
[7] D. Sarafinchan, P.K. Jones, K. Buckley-Golder, H. David, Powder Metal Bearings and Gears with Steel Like Performance, SAE 2001-01-0401, Michigan, 2001.
[8] Y. Takeya, T. Hayasaka, M. Suzuki, Surface Rolling of Sintered Gears, Metal Powder Report, p467-470, Sep 1982.
[9] G. Rau, L. Sigl, M. Krehl, Highly Loaded PM Gears Produced by Selective Surface Densification, SAE 2003-01-0334, Michigan, 2003.
[10] R. Slattery, F. Hanejko, PM of High Density Helical Gears, Advances in Powder Metallurgy and Particulate Materials, Part 9, p56-72, MPIF, Las Vegas, 2003.
[11] S. Bengtsonn, L. Forden, M. Bergstrom, High Performance Gears, Advances in Powder Metallurgy and Particulate Materials, Part 12, p27-34, MPIF, Chicago, 2004.
[12] W. Jandeska, G. Hoffman, R. Slattery, F. Hanejko, A. Rawlings, T. Murphy, Rolling Contact Fatigue of Surface Densified Material: Microstructural Aspects, Advances in Powder Metallurgy and Particulate Materials, Part 10, p35-52, MPIF, Chicago, 2004.
[13] Handbook of Practical Gear Design, D.W. Dudley, CRC Press, 1994.
[14] Theory of Elasticity, 3rd Edition, S.P. Timoshenko, J.N. Goodier, p409-420, McGraw-Hill, New York, 1970.
[15] Advanced Mechanics of Materials, 5th Edition, A.P. Boresi, R. J. Schmidt, O.M. Sidebottom, p692-731, J.Wiley & Sons, New York, 1993.
[16] J.O. Smith, C.K. Liu, Stresses Due to Tangential and Normal Loads on an Elastic Solid with Application to Contact Stress Problems, J. App. Mech. v20, n2, June 1953.
[17] C.J.Yu, T. Prucher, Measuring Youngs Modulus and Shear Modulus – A Comparison of Dynamic and Mechanical Techniques, Advances in Powder Metallurgy and Powder Technology, v1, p272-286, MPIF, Tennessee, 1993.
[18] Materials Standards For PM Structural Parts, Standard 35, MPIF, 2003.
[19] I. Jubault, J.L. Mansot, P. Vergne, D. Mazuyer, In Situ Pressure Measurements Using Raman Microspectroscopy In Rolling Elastohdrodynamic Contact, J. of Tribology, v124, n1, p114-120, Jan 2001.
[20] Gear Design AE15 Manufacturing and Inspection Manual, p34-56, SAE, 1990.
[21] Appearance of Gear Teeth – Terminology of Wear and Failure, American National Standard, ANSI/AGMA 1010-E95, AGMA, 1995.
[22] R. Pederson, S.L. Rice, Case Crushing of Carburized and Hardened Gears, p370-380, Trans SAE, 1961.
[23] The Influence of Microstructure on the Properties of Case-Carburized Components, G. Parrish, p140-165, ASM, 1980.
[24] R.F. Kern, Selecting Steels for Carburized Gears, Metal Progress, v102, n1, p53-64, July 1972.
[25] Design Guide for Vehicle Spur and Helical Gears, American National Standard, ANSI/AGMA, 6002-B93, AGMA, 1993.
[26] V.K. Sharma, G.H. Walter, D. H. Breen, An Analytical Approach for Establishing Case Depth Requirements in Carburized Gears, Publication #77-DET-152, ASME, 1977.
[27] K. Funatani, Residual Stress and Fatigue Strength of Carburized Steels and Gears, SAE 2002-01-1559, Michigan, 2002.
[28] G. Albertini, G. Bruno, F. Fiori, M. Marcantoni, F. Turquier, Residual Stresses in Case Hardened Automotive Steel Gears, Mat. Sci. Forum, Vols. 404-407, p191-196, 2002.
[29] Metals Handbook v1, Properties and Selection of Metals,8th Edition, p108-110, ASM, 1961.
[30] Fundamentals of Metal Fatigue Analysis, J.A. Bannantine, J.J. Comer, J.L. Handrock, p244-254, Prentice Hall, NJ, 1990.
[31] J.J. Coy, C.H. Chao, A Method of Selecting Grid Size to Account for Hertz Deformation in Finite Element Analysis of Spur Gears, J. Mech. Des. ASME Trans, v104, n4, p759-766, 1982.
[32] R. W. Cornell, Compliance and Stress Sensitivity of Spur Gear Teeth, ASME, J. Mech. Des. v103, n2, p447-459, April 1981.
[33] Fundamental Rating Factors and Calculation Methods for Involute Spur and Helical Gear Teeth, American National Standard, ANSI/AGMA, 2001-C95, AGMA, 1994.
[34] Rolling Contact Fatigue Testing of Bearing Steels, Ed. J.J.C. Hoo, STP 771, ASTM, 1982.
[35] J.P. Sheehan, M. Howes, The Effect of Case Carbon Content and Heat Treatment on Pitting Fatigue of 8620 Steel, SAE 720268, 1972.
[36] D. I. Fletcher, J. H. Beynon, Development of a Machine for Closely Controlled Rolling Contact Fatigue and Wear Testing, J. Testing & Eng. v28, n4, p267-275, 2000.
[37] Mechanical Design Handbook, Ed. H. A. Rothbart, p19.35, McGraw-Hill, 1996.
[38] E. E. Bisson, W.J. Anderson, Advanced Bearing Technology” NASA SP-38, National Aeronautics and Space Administration, 1964.
[39] K.L. Johnson, D. Tabor, Rolling Friction, Proc. Inst. Mech. Eng., v182, part 3a, p168, 1967/1968.
[40] K. Lipp & G. Hoffmann, Design For Rolling Contact Fatigue, Advances in Powder Metallurgy and Particulate Materials, part 5, p28-52, MPIF, Orlando, 2002.
[41] Roark’s Formulas for Stress and Strain, 6th Edition, W.C. Young, p647-663, McGraw-Hill, 1975.
[42] Y. Itoh, Y. Takeda, N. Motooka, Y. Kureha, Improvement of the Rolling Contact Fatigue Strength of Sintered Steel for Transmission Component, SAE 890412, Michigan, 1989.
[43] T. Prucher, H. Sanderow, Surface Fatigue of PM Alloys, Advance in Powder Metallurgy and Powder Technology, v2, p99-111, MPIF, Toronto, 1994.
[44] C.M. Sonsino, K. Lipp, Rolling Contact Fatigue Properties of Selected PM Materials for Gear Box Applications, SAE 1999-01-0333, Michigan, 1999.
[45] K. Michealis, FZG, Munich, priv. com. (test rig detail), Dec 2004.
[46] R. Link, G. Kotthoff, Suitability of High Density Powder Metal Gears for Gear Applications, Gear Technology, p15-18, Jan/Feb 2001.
[47] C. Bugiel, WZL, Aachen, priv. com. (test rig detail), Dec 2004.
[48] H. Sanderow, D. McPherson, The Rolling Contact Fatigue Properties of PM Steel Alloys, Advances in Powder Metallurgy and Particulate Materials, part 5, p53-74, MPIF, Orlando, 2002.
[49] G.M. Hamilton, L.E. Goodman, The Stress Field Created by a Circular Sliding Contact, J. App. Mech. V33, n2, p371-376, 1966.
[50] G. Hoffmann, C.M. Sonsino, K. Michaelis, Rolling Contact Fatigue – Component Design and Testing for PM Applications, SAE 1999-01-0332, Michigan, 1999.
[51] S. Ito, N. Tsushima and H. Muro, Accelerated Rolling Contact Fatigue Testing by a Cylinder to Ball Rig, Rolling Contact Fatigue Testing of Bearing Steels, Ed J.J.C.Hoo, p125-135, STP 771, ASTM 1982.
[52] T.M. Clark, G.R. Miller, L.M. Keer, H.S. Cheng, The Role of Near Surface Inclusions in the Pitting of Gears, ASLE Trans, 1984.
[53] I. Sugiura, S. Ito, N. Tsushima and H. Muro, Investigation of Optimum Crowning in a Line Contact Cylinder to Cylinder Rolling Contact Fatigue Test Rig, Rolling Contact Fatigue Testing of Bearing Steels, STP 771, Ed. J.J.C. Hoo, p136-149, ASTM, 1982.