Understanding the Basic Principles of Power Skiving

The interest and successful application in power skiving is increasing within the gear manufacturing community as well as within companies that have access to modern five-axis machines but, thus far, have outsourced their gear manufacturing. The initial solution was developed and patented in 1910 in Germany [1]. Following a somewhat dormant period, a U.S. patent was granted about 60 years later [2]. The same Japanese authors also published a JSME (Japan Society of Mechanical Engineers) paper [3] where they describe gear skiving as a “high productivity method to produce internal gears with rotating tool.” There were few published works until about 2010 when literature appeared in forums such as The International Academy for Production Engineering (CIRP), International Journal of Advanced Manufacturing, American Society of Mechanical Engineers (ASME), and others, where power skiving was dissected and explained in sometimes quite heavy mathematical terms.

Still, an understanding of even the basic principles may not be common knowledge within either the gear manufacturing or the general machining community. This article explains the fundamentals of power skiving in order to guide manufacturing engineers and decision-makers to determine when power skiving can be a suitable solution by using some simple mathematics and rules of thumb.

The recent development in machine controls, machine hardware, and tool design have made it possible to apply the idea from 1910 on an industrial scale for making gears and splines. Software now exists to define the form of the tool and the resulting component geometry, yet no basic rules of thumb or formulas are available in handbooks for the gear manufacturing engineer wanting to make a fast analysis on the viability of power skiving a particular component. To make power skiving a widely used method in gear and spline production, basic understanding of the method is needed.

To demystify power skiving, the following provides approximate yet valid ways to calculate required spindle speeds, which is key in machine and tool selection, as well as guidelines on what components are suitable for power skiving.

Introduction

A variety of methods exists for efficient gear manufacturing such as hobbing, gashing, and broaching. Hobbing is only possible for external gears, while gashing is only possible for larger size internal ring gears from 6 inches (150 millimeters) and up to several feet in diameter using a special head in the hobbing machine. Broaching is a fast and efficient method for internal gears and is well-suited for gears smaller than 8 inches, but is inflexible and uses large tools. A common way of making internal gears is shaping, which is a reciprocating method that’s much slower than both broaching and power skiving. Power skiving is being seen as a viable alternative to broaching to manufacture internal gears (and external gears) since it is faster and more flexible than the other methods.

The Process

Power skiving is a continuous machining process where the tool meshes with the gear being made — similar to the way a pinion and gear mesh in a gear train. This is the reason that an extremely accurate synchronization is needed between the workpiece spindle and the tool spindle. The difference is, while the tool that we can consider “the pinion” meshes with the gear, it is also pushed axially in the direction of the axis of the gear. The front side of the tool (“pinion”) is sharp, and it cuts the gear while meshing. The cutting speed is generated by an inclination “E” between the axis of the gear being made and the axis of the tool. Figure 1 shows the tool (on the left) inclined with respect to the ring gear; both are spinning at high speed while meshing perfectly. The cutting action occurs on the front side of, in this case, the inserted cutting tool. The fixture has openings around the spindle for chip evacuation.

Here, basic mathematics is provided to explain power skiving principles in an intuitive way. Mathematically more stringent explanations can be found in literature, for example, Reference [4].

The cutting speed vc (the relative speed between the front face of the cutting tool and the gear being made) is proportional to the inclination “E” between the tool axis and the gear axis (see Figure 1 and Figure 2), and the peripheral speed v₁ in the point of contact of the tool (“pinion”) and the gear.

If the axis of the tool and the gear being made are parallel, there is no cutting speed being generated. Imagine a pinion meshing with a ring gear with collinear axes; there will be no speed between the front face of the pinion and the ring.  More inclination means more cutting speed at the same peripheral speed v₁. As the rotational speed is proportional to the peripheral speed, a higher inclination reduces the needed rotational speed of the tool and workpiece, with a maximum possible angle at 45 degrees. This can be, as explained later, beneficial in order to keep the process within machine limitations.

The following are two worked-out examples of spindle speed analysis. The calculations are approximations of spindle speeds valid for spur gears and straight splines. The equations are valid for any case as long as metric units are used throughout. The background to these equations and their parameters will be explained later.

Example 1:

In this example, a small workpiece with a 1-inch diameter is analyzed for necessary spindle speeds using a solid HSS cutter.

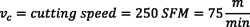
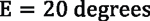
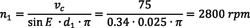
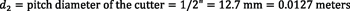
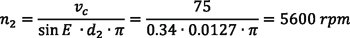
Example 2:

In this example, a workpiece with a 10-inch diameter is analyzed for necessary spindle speeds using a carbide insert cutter.

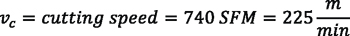
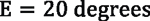
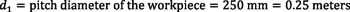
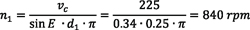
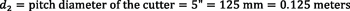
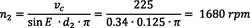
To find these equations, begin with the equation that relates peripheral speed with cutting speed:

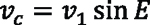
By rearranging, the needed peripheral speed can be calculated as:

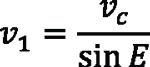
The peripheral speeds in the meshing point are equal between the tool and the gear being made, but in different angular directions, meaning that

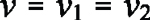
where the second speed is the peripheral speed of the tool. This can be seen in Reference [4], which describes this in a much more detailed way. The purpose here is to be able to quickly estimate needed spindle speeds when choosing a machine, not for optimizing the process. The general relationship between peripheral speed and rotational speed is

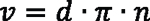
or rearranged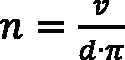

using the aforementioned equation and substituting, so we get:

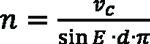
Knowing the respective pitch diameters of gear d₁ and tool d₂, it is possible to calculate the needed rotational speeds n₁ and n₂ of the workpiece and the tool, respectively, to create the desired cutting speed. Spindle speeds will be:

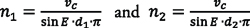
which are the equations used in examples 1 and 2.

Accurate synchronization between the tool and the gear being generated is of utmost importance. The relationship between the rotational speeds between the tool and gear being generated is proportional to their respective pitch diameters or tooth counts. Envision a gearbox where the shafts would not spin exactly at the intended ratio; it would not work. Even a slight mismatch in rotational speed causes major problems. A difference of only 1 rpm between the tool and the gear produced means that, in 30 seconds of power skiving machining, the mismatch would be 1/2 of a revolution. In practice, small mismatches result in vibrations and bad surface; large mismatches result in severe crashes. Hence, you should not try to use a machine incapable of synchronizing at high rpm for power skiving. Even in capable machines, it is recommended to start with plastic or machinable wax.

The Cross Angle

As seen, using a higher cross angle reduces the spindle speeds (up to 45 degrees). Since one of the biggest hurdles in power skiving is maintaining synchronization at high spindle speeds, a larger angle is therefore beneficial.

What limits the inclination is usually the workpiece and, in some cases, the machine. An internal gear with a large face width and a small diameter will, for example, not permit a high inclination since the tool extension would collide with the side of the workpiece/gear itself. Because high rigidity is needed for a successful process, the extension diameter should be as close as possible to the tool diameter. Increasing the shaft angle by using a small diameter extension is hence not a good way to proceed, since the advantage of reduced spindle speeds is soon overtaken by the loss in rigidity. The toolmaker should help in evaluating the best combination of tool diameter and cross angle to optimize the process within the machine limitations. A typical cross angle for internal parts is 20 degrees — an ideal compromise of clearance and cutting speed at “reasonable” spindle speeds.

As a rule of thumb, power skiving becomes difficult when the depth of the splined area is larger than the internal diameter of the part. Some driveline splines have a small diameter where the length of the spline can be two times or more the internal diameter. Such components are not suitable for power skiving.

For external gears, the shaft angle is not as restricted by the workpiece, and a higher shaft angle can be used, up to 45 degrees. For a long, slender part, a higher shaft angle will help to clear the machine spindle head and permit a shorter overall tool length, which is positive for rigidity. As explained earlier, a high shaft angle reduces the needed spindle rpms, too.

Another limiting factor for the shaft angle is, the higher the shaft angle, the more clearance is needed after the gear teeth. The center of the cutter needs to cut all the way through the thickness of the gear, hence the cutter will protrude below the gear. The needed clearance (see Figure 2) is dependent on inclination and tool radius r₁:

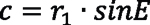
Tool Requirements

The power skiving tool needs to be designed so that the correct tooth form is created. By the nature of the process, each tool will make a specific module or diametral pitch (DP) and a specific tooth count. It is not like in hobbing where the same hob can make several tooth counts; rather, it is more like a disc cutter where each disc will make a certain tooth form. Furthermore, the shape of a power skiving tool is not the same as a shaping tool, despite the similarity at first sight.

Here, it’s important to mention again the need for high spindle speeds in perfect synchronization. Looking at the governing equation, the smaller the diameter of the workpiece, the higher the rpm required.

Referring back to example 1, for a 1-inch part using an HSS cutter, spindles spinning at 2,800 rpm and 5,600 rpm respectively need to be synchronized. In example 2, for a 10-inch part, an inserted cutter (or solid carbide cutter) can be used, since the required rpm for a larger workpiece diameter is lower.

At the time of writing, the numbers in the examples are achievable with machines available in the market.

For parts having DP10 and larger tooth forms, inserted cutters are possible to apply. There are advantages to using inserted tools for larger tooth forms. Solid carbide tools especially are increasingly costly, and damage to one tooth in a solid cutter usually means scrapping it, while a damaged insert can be changed (see Figure 3). Also, the carbide grade and coating of inserts can be optimized more than solid carbide tools, since there’s no stripping and regrinding needed. The same cutter body can be used while different inserts are tested in order to find the best solution, for example, in the case of a difficult material, such as in aerospace applications. The possibility to exchange inserts instead of regrinding also means less inventory and less logistics, simplifying the manufacturing process.

Machine Requirements

Choosing the right machine for the machining process is crucial, especially since power skiving is an unforgiving process; minor errors in synchronization or lack of rigidity will quickly adversely affect the gear quality or, worse, lead to a crash. Small errors in synchronization will lead to waviness on the gear flanks. It should not be assumed that the machine can synchronize at any speed of the respective spindle. It is possible that the tool and workpiece spindles individually can run at the needed speeds according to the aforementioned equations; however, it is not at all certain they can run in virtually perfect synchronization at those speeds. While the specifications may show that the tool spindle can spin at 6,000 rpm and the workpiece at 3,000 rpm, it does not necessarily mean they can synchronize at those speeds. A machine can be perfectly capable to turn or do some turn milling, but power skiving requires a whole other level of synchronization.

Usually, it is the workpiece spindle that is the limiting factor. The smaller the workpiece and the smaller the inclination, the faster the spindle must run to generate enough cutting speed.

As shown in examples 1 and 2, it is possible to evaluate spindle speeds up to which synchronization is required. Knowing the desired cutting speed, the shaft angle, and the pitch diameter of the gear is sufficient to calculate the speed of the workpiece.

For a given workpiece, there are only two ways to bring the rotational speeds to a level where the machine can synchronize: either increase the shaft angle (up to 45 degrees) or reduce the cutting speed. The shaft angle is usually limited to about 20 degrees for internal gears and splines due to collision. Tools need a minimum speed to cut properly, and a tool manufacturer will know the boundaries.

Cutting Strategies

While this article serves as a guide in the basic selection of a machine and tool to manufacture a part with power skiving, a detailed explanation of the cutting strategies and detailed cutting data is outside the article’s scope, but the following presents some general guidelines:

Depth of Cut: Power skiving demands both high accuracy in synchronization, as previously mentioned, and high stiffness. To avoid exceeding any of these requirements, several passes are necessary except for the smallest gears or splines. Through tests, a logarithmic decrease in cutting depth has been shown to work well.

Choosing the Feed Strategy: Choosing the right feed in power skiving depends on the component and cutter. Targeting a specified chip thickness per tooth at the cutter has shown to be a good way to determine the total linear feed of the cutter.  Mathematical analysis beyond the scope of this article exists to determine the suitable linear feed.

A caveat is, once waviness has occurred, it will not be possible to remove with a finishing pass, since the uneven flanks will cause variation in cutting forces that leads to further waviness.

Suitable Components

There are rules of thumb that can be used to evaluate suitable components for power skiving. (For external gears or splines, always consider disc cutting or hobbing.) The following basic checklist can help determine if a component is a good candidate for power skiving.

• Diameter-to-depth ratio is 1 or larger (for internal gears).
• There is needed clearance at the bottom of cutter radius x sin(cross angle) + extra for over-travel.
• Pressure angle is 18 degrees or larger (less is possible, but harder).
• Rounded root or root with fillets.

This is a first basic test, but a deeper investigation needs to be made using simulation software that will show the tool form and resulting tooth form and will analyze for collisions.

Every power skiving case should be seen as a project where the combination of a workpiece, a machine, and a tool need to be investigated before purchasing anything. First, start with the workpiece, design a suitable tool, and then determine what machine is required. A capable tool manufacturer can lead this project together with the gear producer.

Alternatives to Power Skiving

While the interest for power skiving is ever-increasing, it is, however, important to consider alternatives. Power skiving requires machine investments as well as deep application knowledge to succeed. Hobbing requires specialized machines or special cycles in a CNC machine as well as good stability of the machine and setup. Hence, for external parts, disc cutting “slotting” with ground-to-form inserts should always be considered. That solution has the advantages of exchangeable carbide inserts (no regrind, high cutting speed, and capable of cutting difficult materials). For a spur gear or straight spline, it is a straight cut, so it requires only a four-axis machine (or a three-axis machine with a rotary table) and no special cycles. For a helical, a five-axis machine or a four-axis with a head with the ability to tilt the cutter is needed, and still no special cycles are needed.

Disc cutters (Figure 4) enable companies that have old, outdated hobbing machines using HSS hobs to transfer that work to more modern CNC machines, thereby consolidating more operations with the same machine. This can also benefit companies currently outsourcing gears and splines and allow them to instead manufacture parts in-house without large investments in hobbing machines or machines capable of power skiving. Power skiving can then follow when there is a need for internal parts and a willingness to invest in machines and training.

Conclusion

Power skiving is an interesting process particularly for internal splines and gears and for external parts where the clearance to a shoulder is limited but existing. Careful considerations have to be made before purchasing a machine, especially with respect to perfect synchronization at high spindle speeds. The tools need to be designed to accommodate both the workpiece geometry and the machine (including rpm limitations). Additional consideration of the tool form, tool diameter, extensions, workpiece setup, and chip evacuation strategy needs to be made as well as considering if a solid or inserted tool is most suitable.

References

1. V. Pittler, Verfahren zom Schneiden von Zahnrädern mittels eines zahnradartiges, an den Stirnflächen der Zähne mit Schneidekanten versehenen Schneidwerkzeugs, Deutsche Patentschrift Nr. 243514, W. (1910).
2. K. Nishijima and M. Kojima, Skiving cutter for use in cutting internal spur gear, U.S. patent 4066001. (1974).
3. K. Nishijima and M. Kojima, Gear Skiving of Involute Internal Spur Gear: (Part 1. On the Tooth Profile). Bulletin of JSME 17(106), 511-518, 1974, The Japan Society of Mechanical Engineers (1974).
4. E. Guo et al., Research on the cutting mechanisms of cylindrical gear power skiving. Journal of Advanced Manufacturing Technology (2015) 79:541-550 DOI 10. 1007/s00170-015-6816-9 (2015).

Acknowledgments: The author would like to acknowledge the expertise and support received from Sandvik Coromant employees: Mats Wennmo, Sture Sjöö, Brent Marsh, Mark Briel, and Mikael Lundblad for their work with power skiving.