Planetary Gear Parametric Instability

Parametric instability is investigated for planetary gears where the fluctuating stiffness results from the changing contact conditions at the multiple tooth meshes. The time-varying mesh stiffnesses of the sun-planet and ring-planet meshes are modeled as rectangular waveforms with different contact ratios and mesh phasing. The operating conditions leading to parametric instability are analytically identified. Using the well-defined properties of planetary gear vibration modes, the boundaries separating stable and unstable conditions are obtained as simple expressions in terms of mesh parameters. These expressions allow one to suppress particular instabilities by adjusting the contact ratios and mesh phasing. Tooth separation from parametric instability is numerically simulated to show the strong impact of this nonlinearity on the response.

Introduction

Mesh stiffness variation as the number of teeth in contact changes is a primary excitation of gear vibration and noise. This excitation exists even when the gears are perfectly machined and assembled. In analytical gear vibration models, it is represented by time-varying mesh stiffnesses that parametrically excite the system. This parametric excitation causes instability under certain operating conditions. The ensuing vibration creates noise, increases dynamic loads, and potentially damages the gear teeth and bearings [1].

Parametric instability in single-pair gears governed by a single degree-of-freedom Mathieu equation has been extensively investigated [2-6]. For multi-stage gear systems, there are surprisingly few studies on parametric instabilities from multiple meshes. Tordion and Gauvin [7] and Benton and Seireg [8] analyzed the instabilities of two-stage gear systems with a mesh phasing between the two mesh stiffnesses. However, their instability conclusions are contradictory. This was recently clarified by Lin and Parker [9] using perturbation and numerical analyses. Lin and Parker also derived simple formulae that allow designers to suppress particular instabilities by properly selecting contact ratios and mesh phasing. For planetary gears ( Figure 1), which have multiple time-varying mesh stiffnesses, no systematic study on their parametric instability has been found in the literature. August and Kasuba [10] and Velex and Flamand [11] numerically computed dynamic responses to mesh stiffness variations for planetary gears with three sequentially phased planets. Their results showed the dramatic impact of mesh stiffness variation on dynamic response, tooth loads, and load sharing among planets. In addition, different contact ratios and phasing conditions that exist at the multiple meshes complicate the analytical examination of planetary gear parametric instability. How these factors affect instability conditions has not been investigated.

The objective of this study is to analyze parametric instability excited by multiple time-varying mesh stiffnesses in planetary gears [21]. The torsional vibration model used here considers the different contact ratios and planet phasing among multiple meshes, which are critical design parameters in planetary gears. The well-defined modal properties of planetary gears [12, 13] are used to derive simple expressions for instability boundaries separating the stable and unstable regions. From these expressions, the effects of contact ratios and mesh phasing are analytically determined. These results provide insight into planetary gear designs that avoid parametric instability. In practice, planet mesh-phasing schemes are often applied to cancel or neutralize resonant response at speeds where the mesh frequency is near a natural frequency [14-17]. In this same spirit, this study shows that particular parametric instabilities can be eliminated under certain phasing conditions that can be achieved by proper selection of design parameters. Tooth separation nonlinearity induced by parametric instability is numerically simulated and shown to have great impact on the unstable system response.

System Model and Model Properties

The planetary gear dynamic model used is based on the one developed by Lin and Parker [12].Translational degrees of freedom in that model are eliminated, and only rotational motions of the gear bodies are considered ( Figure 1). Rotational motions of the carrier, ring, sun, and planets are denoted by θ_h, h=c,r,s,1,…N, where N indicates the number of planets. The gear bodies are assumed rigid with moments of inertia I_c, I_r, I_s, I_p. The sun-planet and ring-planet tooth meshes are modeled as linear springs with time-varying stiffnesses k_sn(t), k_rn(t), n=1,…N. Damping and clearance nonlinearity are not considered in the determination of instability boundaries, though they are added later in a numerical example for response calculation. The system equations of motion are

(1)

(2)

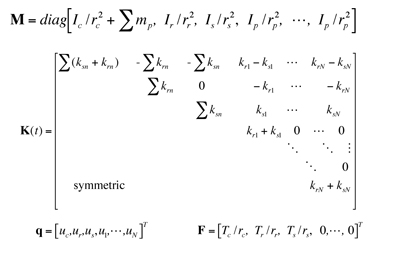
where the summation index n ranges from 1 to N. u_h=r_hθ_h, h=c,r,s,1,…N are base radius deflections, and r_h is the base circle radius for the sun, ring, and planets and the radius of the circle passing through the planet centers for the carrier. T_c, T_r, T_s are external torques. Each mesh stiffness is represented by where k_sp, k_rp are mean values and k_1n, k_2n are time-varying components of the n-th sun-planet and ring-planet meshes. Expansion of k_1n, k_2nin Fourier series yields

(3)

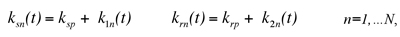
where k_sp, k_rp are mean values and k_1n, k_2n are time-varying components of the n-th sun-planet and ring-planet meshes. Expansion of k_1n, k_2nin Fourier series yields

(4)

For spur gears, rectangular waves are often used to approximate mesh stiffnesses alternating between d and d+1 pairs of teeth in contact. Figure 2 shows the mesh stiffness variations k_1n, k_2n with peak-to-peak amplitudes 2k_vs, 2k_vr, contact ratios c_s, c_r, and phasing angles ϒ_snT, (ϒ_sr+ϒ_rn)T. The sun-planet and ring-planet meshes have the identical mesh frequency Ω=2π/T. The sun-planet mesh stiffnesses between planets differ only by a time translation (or phase), i.e. k_sn(t)=k_s1(t-ϒ_snT). Likewise, k_rn(t)=k_r1(t-ϒ_rnT) for the ring-planet meshes. Mesh phasing between planets is determined by planet position angles ψ_n and the numbers of teeth z_s, z_r for the sun and ring [15]. ϒ_sn=ψ_nz_s /(2π) denotes the mesh phasing between the first and n-th sun-planet meshes (ϒ_s1=0); ϒ_rn=-ψ_nz_r /(2π) is the mesh phasing between the first and n-th ring-planet meshes (ϒ_r1=0); for any planet, ϒ_sr is the phasing between the sun-planet and ring-planet meshes for a given planet; It is the same for each planet. The Fourier coefficients in (4) are

(5) 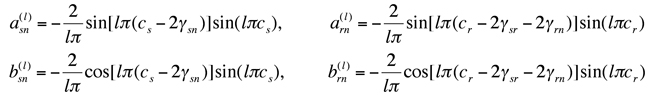Mesh stiffnesses depend on many parameters including the number of teeth in contact, gear facewidth, material properties, profile modifications, and applied load [18]. Let and be the relative amplitudes of mesh stiffness variation. In the simplest approximation, mesh stiffnesses are assumed proportional to the number of tooth pairs in contact, that is, k_sp=c_s k_1t, k_rp=c_r k_2t and k_vs= k_1t /2, k_vr= k_2t /2, where k_1t, k_2t are one-pair tooth bending stiffnesses of the sun-planet and ring-planet meshes. With this simplifying assumption, the nominal amplitudes of stiffness variations are ε₁=1/(2c_s), ε2=1/(2c_r), and one obtains the explicit relation ε₂=ε₁ c_s /c_r. In practice and in the analysis that follows, however, ε₁ and ε₂ are not constrained to these “nominal” values but vary independently of the contact ratios to account for the many factors influencing mesh stiffness variation amplitudes. For this modeling, we let ε₁=ε₂/g=ε where g=O(1) (and g=c_s /c_r under the simplifying assumption noted above). Substitution of (3) and (4) into (2) yields

(6)

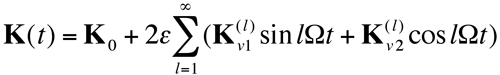
where the average stiffness matrix K₀ has the same form as (2) with k_sn, k_rn substituted by k_sp, k_rp. The Fourier coefficient matrices are also in the form (2) with k_sn, k_rn substituted by

for for and substituted by

For the time-invariant case, the eigenvalue problem associated with (1) is

(7)

where ω_i are the natural frequencies. The vibration modes φ_i are normalized as Φ^TMΦ=I with Φ=[φ₁,…,φ_L]. The natural frequencies and vibration modes have unique properties due to the cyclic symmetry of planetary gears [12, 13]. We specialize these properties for the case of a rotational vibration model with fixed ring and L=N+2 degrees of freedom. In this case, all vibration modes can be classified into one of three categories: (1) a rigid body mode (ω₁=0), (2) two modes with distinct natural frequencies (ω₂, ω_L), and (3) a group of degenerate modes with multiplicity N–1 (ω₃=…=ω_N+1). In the distinct modes, including the rigid body mode, all planets have identical motion

(8)

In the degenerate modes, the carrier, ring, and sun have no motion, and the planet rotations satisfy

(9)

These well-defined properties are valid not only for equally spaced planets with position angles ψ_n =2π(n-1)/N, but also for diametrically opposed planets with ψ_n+N/2 = ψ_n +π [13].

General Expresion for Instability Boundries

Parametric instabilities occur when harmonics of the mesh frequency are close to particular combinations of the natural frequencies. We determine the operating conditions (that is, mesh frequency Ω and stiffness variation amplitude ε) that lead to instability when l Ω≈ω_p+ω_q for integer l. The results are illustrated as stable and unstable regions in the (Ω, ε) parameter plane (Figure 3, for example).

Primary (l=1, p=q), secondary (l=2, p=q), and combination (l=1, pq) instabilities are of most interest as higher order instabilities have much smaller instability regions and are unlikely to occur in practice. The rigid body mode (ω₁=0) is not excited under operating conditions and does not affect the instabilities of other modes. Only the two distinct modes and the group of degenerate modes are considered in what follows. Applying the modal transformation q=Φz to (1) and using (6), the free vibration equations become

(10)

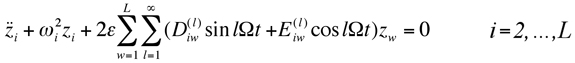
where the matrices and . Using the method of multiple scales, the solution of (10) is expressed as

(11)

where τ=εt and . Substitution of (11) into (10) yields

(12)

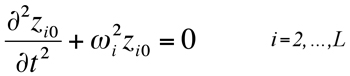
(13)

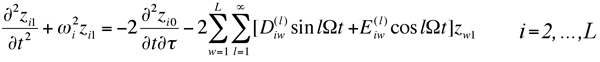
The general solutions of (12) are

(14)

where cc represents the complex conjugate of preceding terms. Insertion of (14) into (13) yields

(15)

The parametric instability when l Ω≈ω_p+ω_q is considered. Let , where σ is a detuning parameter to be determined. When ω_p and ω_q are both distinct, the instability boundaries are [9]

single mode instability: (16)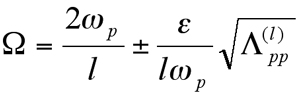

combination instability: (17)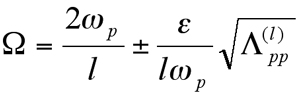

where.

When ω_p or ω_q is degenerate, the complexity of instability boundary solutions depends on the multiplicity of the degenerate natural frequencies. We first study the case with multiplicity two for three-planet systems, say ω_p=ω_q. For the single-mode instability , vanishing of the terms in (15) leading to unbounded response requires

(18)

(19)

The nontrivial solutions of (18) and (19) have the form

(20)

where R_p, R_q, I_p, I_q are real. With these solutions, (18) and (19) yield

(21)

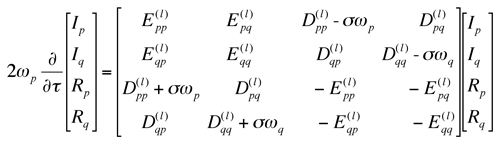
For bounded solutions, the eigenvalues of the coefficient matrix have non-positive real parts, which requires

(22)

Thus, the single-mode instability boundaries for ω_p=ω_q are

(23)

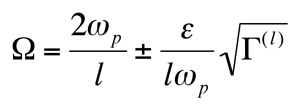
Now consider the combination instability where ω_p=ω_q are degenerate but ω_r is distinct. Vanishing of the terms in (15) leading to unbounded response requires

(24)

(25)

(26)

With the solutions (20) and , (24)-(26) give

(27)

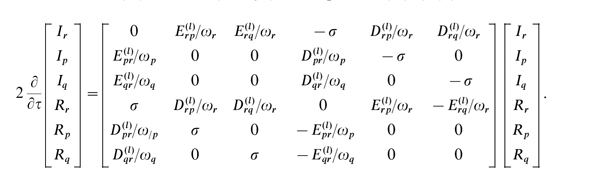
Requiring the eigenvalues of the coefficient matrix to have non-positive real parts gives the instability boundaries

(28)

When the degenerate natural frequencies ω₃=…=ω_m+2 have multiplicity m > 2, vanishing of the terms in (15) leading to unbounded response for l yields m coupled equations

(29)

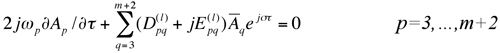
Similar to (21), a 2m×2m coefficient matrix is obtained from (29)

(30)

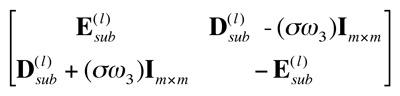
where are mxm submatrices of including rows and columns 3, …, m+2. The σ for bounded solutions is obtained by requiring the real parts of the eigenvalues of this coefficient matrix to be non-positive. Generally, no closed-form solution can be derived for these single-mode instabilities, but numerical evaluation can determine σ and the instability boundaries unless have special features (e.g., diagonal matrices) as discussed later. More is possible for combination instabilities. For combination instability of distinct ω_r and degenerate ω₃=…=ω_m+2 of any multiplicity m, the same procedure as led to (28) yields instability boundaries

(31)

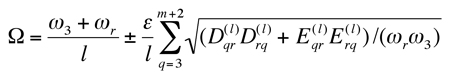
All results so far apply for a general system (10) with degenerate natural frequencies. These results reduce to simple forms when specialized to planetary gears.

Planetary Gear Parametric Instability

Planetary gears′ well-defined modal properties are now used to simplify the above instability conditions to compact expressions suitable for use in applications. Expansion of in (10) gives

(32)

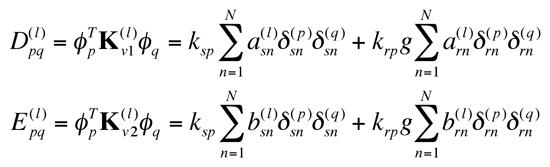
where is the deformation of the n-th sun-planet mesh in mode φ_p and is the deformation of the n-th ring-planet mesh. For different spacing and phasing of planets, matrices have special features that simplify the instability conditions. Note the following analysis considers mesh stiffness of any waveform as represented by the Fourier coefficients a, b in (32). As the most appropriate analytical idealization for spur gears, rectangular waveforms (5) are used to get simplified expressions and investigate the effects of contact ratio and phasing.

Equally Spaced Planets

For equally spaced planets (ψ_n =2π(n-1)/N), the vibration modes have structured properties (8) and (9). In this case, (z_s+z_r)/N = integer and the planet meshes have phasing ϒ_sn=(n-1)z_s /N and ϒ_rn=-(n-1)z_r /N, n=1,…,N. The two possible phasing conditions are examined below.

(1) In-phase Planet Meshes

Consider the case when all the sun-planet meshes are in-phase (ϒ_sn=0, n=1,…,N) and all the ring-planet meshes are in-phase (ϒ_rn=0, n=1,…,N). This design is typical when optimizing load sharing among planets and results when z_s and z_r are each integer multiples of N. There is, however, a constant phasing ϒ_sr between the sun-planet and ring-planet meshes for each planet. The Fourier coefficients in (4) and (32) are independent of the planet index n for in-phase planet meshes.

For a distinct natural frequency ω_p, vibration mode property (8) leads to for any planet n. Using rectangular form (5) and (32) in (16), the primary instability boundaries are governed by

(33)

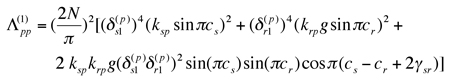
Obviously, = 0 when c_s, c_r are integers and all instabilities vanish. If c_s, c_r integer, a second choice to reduce the instability regions is to make the third term in (33) negative by adjusting c_s, c_r, and ϒ_sr. The combination instability boundaries for two distinct modes can be obtained from (17).

For the degenerate natural frequencies ω₃=…=ω_N+1, vibration mode property (9) results in

(34)

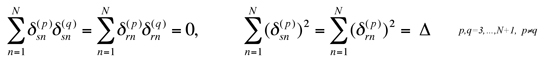
where the following identities are used to derive (34)

(35)

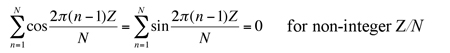
Use of (34) in (32) gives

(36)

For the simple form of in (36), the eigenvalues of (30) can be expressed in closed-form for any multiplicity m=N-1. In this case, the single-mode instability boundaries are the same as (23) with . For the rectangular waveforms (5),

(37)

Equation (37) applies for any number of planets N.

For the combination instability of degenerate ω₃=…=ω_N+1 and distinct ω_r, use of properties (8) and (9) in (32) yields

(38)

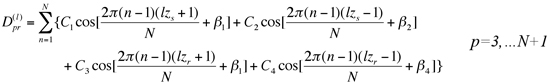
where C_i and β_i are constants independent of n. For in-phase planet meshes (z_s /N, z_r /N are integers) and l=1, (35) guarantees =0 and similarly =0. It follows from (31) that the combination instabilities (l=1) of a distinct mode and a degenerate mode always vanish for any N when the planet meshes are in-phase. A more general condition for vanishing of these combination instabilities is that each of (lz_s±1)/N, (lz_r±1)/N integer.

As an example, Figure 3 shows the instability boundaries for a planetary gear with three equally spaced planets. The parameters and nominal natural frequencies are given in Table 1 and the vibration modes are shown in Figure 4. The mesh phasing ϒ_sn=ϒ_rn=0, ϒ_sr=1/2 and the contact ratios c_s=1.4, c_r=1.6. We specify ε₁=ε₂=ε (that is, g=1). The slight downward drift in the instability regions results from natural frequencies frequency changes as ε varies, which occur because the average mesh stiffnesses depend on k_vs and k_vr; (the central line between the peak-to-peak mesh stiffnesses in (Figure 2) are kept constantsheld constant) in the example (Figure 2). The analytical solutions (solid lines) from (16), (17), (23), and (28) agree well with the numerical solutions using Floquet theory and numerical integration. Note the combination instabilities at ω₂+ω₃, ω₃+ω₅ vanish because they involve the distinct (ω₂,ω₅) and degenerate (ω₃=ω₄) natural frequencies. Figure 5 shows the primary instability regions for different contact ratios c_s, c_r; the stiffness variation amplitude ε=0.3 and phasing ϒ_sr=0. All instabilities vanish when the contact ratios are integers. The size of the 2ω₂ instability region is primarily affected by c_r while insensitive to changes in c_s. This is because the dominant deformation of mode φ₂ occurs in the ring-planet meshes (Figure 4). The 2ω₅ instability region is mostly affected by c_s because most deformation occurs in the sun-planet meshes for this mode. The primary instability of the degenerate modes at 2ω₃=2ω₄ is influenced by both c_s and c_r. The primary instability regions are maximized for c_s=c_r=1.5, which is expected from (33) and (37). The relative phasing ϒ_sr between the sun-planet and ring-planet meshes can have a major impact. When the phasing ϒ_sr=1/2 ( Figure 5), the 2ω₃=2ω₄ instability vanishes for any c_s=c_r because Γ⁽¹⁾ =0 in (37) in this case.

(2) Sequentially Phased Planet Meshes

Here we consider equally spaced planet systems where the sun-planet and ring-planet meshes are sequentially phased with ϒ_sn=(n-1)z_s /N and ϒ_rn=-(n-1)z_r /N. This case corresponds to z_s /N, z_r /N integer but (z_s+z_r)/N=integer. A constant phasing ϒ_sr exists between the sun-planet and ring-planet meshes for each planet. Using (35) and the sequential phasing, the Fourier coefficients in (32) satisfy

(39)

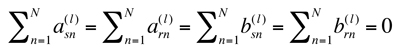
when lz_s /N, lz_r /N are non-integer. Equation (39) applies for any waveform of mesh stiffness variation waveform.

For distinct natural frequencies ω_p, using and (39) in (32) yields . It follows from (16) that the primary instabilities (l=1) of distinct modes always vanish when the planets are sequentially phased. Physically, it means that these instabilities are not excited because the resultant modal excitations from the sun-planet and ring-planet meshes each are zero. The secondary instabilities (l=2) of distinct modes also vanish when 2z_s /N, 2z_r /N are non-integer. Similarly, for combination instability (l=1) of distinct ω_p and ω_q, in (17). Thus, combination instabilities of two distinct modes always vanish in this case.

For instabilities involving the degenerate modes, it is difficult to obtain simple expressions for the instability boundaries; their instability conditions can be calculated from (23), (30), and (31). A special case is the combination instability (l=1) of degenerate ω₃=…=ω_N+1 and distinct ω_r when (z_s±1)/N, (z_r±1)/N each is non-integer. In this case,= =0, p=3,…,N+1 because of (35) and (38), and the combination instabilities of distinct and degenerate modes vanish.

Figure 6 shows the instability boundaries for the same system as in Figure 3 , except the three planets are sequentially phased with ϒ_sn= [0, 1/3, 2/3], ϒ_rn= [0, -2/3, -1/3]. Note the primary, secondary, and combination instability regions vanish for the distinct natural frequencies ω₂, ω₅; only instabilities involving the degenerate modesω₃=ω₄ exist.

The above analyses show that contact ratios and mesh phasing significantly affect the operating condition instability regions. In practice, particular instabilities can be minimized by proper selection of contact ratios and mesh phasing, which are adjusted by center distance, diametral pitch, pressure angle, tooth addendum, numbers of teeth, and other parameters. The foregoing results for equally spaced planets and any mesh stiffness waveform (not just rectangular) are summarized in Table 2.

Unequally Spaced Planets

When the planets are arbitrarily spaced, the structured modal properties do not exist and the general expressions for instability boundaries cannot be further simplified. For the practically important case of diametrically opposed planets, however, the vibration modes retain the well-defined properties (8) and (9). For the sun-planet meshes, each of the N/2 pairs of diametrically opposed planets are in-phase (ϒ_s(n+N/2) =ϒ_sn) for even zs and counter-phased (ϒ_s(n+N/2) =ϒ_sn+1/2) for odd z_s. An analogous rule applies for the ring-planet mesh phasing. Note that adjacent planets have arbitrary mesh phasing defined by their circumferential position, ϒ_sn=Ψ_nz_s /(2π), ϒ_rn=-Ψ_nz_r /(2π), n=1,…,N/2.

When the sun-planet and ring-planet meshes are both counter-phased (odd z_s, z_r), equation (39) holds for odd l because and similar relations for. Recalling modal property (8), for distinct ω_p, ω_q and odd l. From (16) and (17), primary and combination (l=1) instabilities of distinct modes always vanish in the counter-phased case. Physically, these instabilities are eliminated because the modal excitations from each pair of diametrically opposed planets always cancel each other. The instability regions involving degenerate modes are obtained from numerical evaluation of the eigenvalues of (30).

When pairs of opposing sun-planet or ring-planet meshes are in-phase (even z_s or even z_r), no simple expression for instabilities regions is available; numerical solutions are obtained from (16), (17), (30), and (31).

Dynamic Response and Contact Loss

When planetary gears operate inside an instability region, damping and nonlinearities from friction, tooth separation, etc. bound the unstable linear model motion. Figure 7a shows the RMS steady-state planet response amplitude versus mesh frequency for the same system as in Figure 3 and the stiffness variation ε=0.3. Rayleigh damping C=(0.07)*M+(0.07)*K is added to system (1) and the force vector is F=[-2000 1000 0 0 0]^T N. The solutions are obtained from numerical integration of (10) using mesh stiffnesses in rectangular waveforms (Figure 7b). The instabilities near ω₃=ω₄, 2ω₃=2ω₄, and ω₂+ω₅ grow to instability very slowly so that their parametric instabilities are not apparent in Figure 7a (and Figure 8a). The instability excited by the primary instability 2ω₅ grows extremely large because tooth separation (that is, vanishing mesh stiffness) is not considered; the mesh stiffnesses are pre-specified functions of time (Figure 7b). In practice, tooth separation (clearance nonlinearity) occurs for large dynamic responses and its effects are dramatic. Figure 8a shows the response for the same system as in Figure 7a but tooth separations are modeled. The mesh stiffness k_sn or k_rn is set to zero if the corresponding tooth deformation δ_sn<0 or δ_rn<0 at any step of the integration. The response amplitude of the 2ω₅ primary instability is significantly reduced from that in Figure 7a. Moreover, a softening jump phenomenon occurs. Sun-planet tooth separation (k_sp=0) is apparent in Figure 8b for a mesh frequency in the primary instability region of 2ω₅. The interactions of mesh stiffness variation and clearance nonlinearity has been studied by Kahraman and Blankenship [19, 20] for single-mesh gears. Their effects on multi-mesh planetary gears need additional investigation.

Conclusions

This work analytically investigates the parametric instabilities from mesh stiffness variation in planetary gears. Instability boundaries are obtained for systems with equally spaced (summarized in Table 2) and diametrically opposed planets. The main points are:

1. Using the structured properties of vibration modes, the instability boundaries are reduced to simple, closed-form expressions for several planet phasing conditions. The instability boundaries are sensitive to contact ratios and mesh phasing, and the simple expressions are useful in design to suppress instabilities by adjusting these parameters.

2. Certain parametric instabilities always vanish for particular mesh phasing conditions, including (1) combination instabilities of distinct and degenerate modes when equally spaced planets are in-phase, (2) primary and combination instabilities of distinct modes when equally spaced planets are sequentially phased, and (3) primary and combination instabilities of distinct modes when diametrically opposed planets are counter-phased. These features come from the well-defined modal properties and apply to any form of mesh stiffness variation.

3. Instability boundaries relate directly to mesh deformations in the vibration modes. The mesh parameters (e.g, c_s and c_r) that are most critical to a particular instability are those of the tooth meshes with dominant deformations in the unstable vibration modes.

4. When a parametric instability is excited under operating conditions, tooth separation occurs. This nonlinearity dramatically changes the dynamic response. More analysis is needed to reveal the interaction of mesh stiffness variation and backlash nonlinearity in multi-mesh gear systems.

References

1. M. Benton and A. Seireg 1978 Journal of Mechanical Design 100, 26-30. Simulation of resonances and instability conditions in pinion-gear systems.
2. J. G. Bollinger and R. J. Harker 1967 Journal of the Industrial Mathematics 17, 39-55. Instability potential of high speed gearing.
3. M. Benton and A. Seireg 1981 Journal of Mechanical Design 103(2), 372-378. Factors influencing instability and resonances in geared systems.
4. C. Nataraj and N. K. Arakere 1999 ASME Design Engineering Technical Conferences, Paper No. DETC99/VIB-8110, September, Las Vegas, NV. Dynamic response and stability of a spur gear pair.
5. M. Amabili and A. Rivola 1997 Mechanical Systems & Signal Processing 11(3), 375-390 . Dynamic analysis of spur gear pairs: Steady-state response and stability of the sdof model with time-varying meshing damping.
6. C. Nataraj and A. M. Whitman 1997 ASME Design Engineering Technical Conferences, Paper No. DETC97/VIB-4018, September, Sacramento, CA. Parameter excitation effects in gear dynamics.
7. G. V. Tordion and R. Gauvin 1977 Journal of Engineering for Industry 99, 785-791. Dynamic stability of a two-stage gear train under the influence of variable meshing stiffnesses.
8. M. Benton and A. Seireg 1980 Journal of Mechanical Design 102(2), 379-383. Normal mode uncoupling of systems with time varying stiffness.
9. J. Lin and R. G. Parker 2000 Journal of Vibration and Acoustics 124, 68-76. Mesh stiffness variation instabilities in two-stage gear systems.
10. R. August and R. Kasuba 1986 Journal of Vibration, Acoustics, Stress, and Reliability in Design 108(3), 348-353. Torsional vibrations and dynamic loads in a basic planetary gear system.
11. P. Velex and L. Flamand 1996 Journal of Mechanical Design 118, 7-14. Dynamic response of planetary trains to mesh parametric excitations.
12. J. Lin and R. G. Parker 1999 Journal of Vibration and Acoustics 121, 316-321. Analytical characterization of the unique properties of planetary gear free vibration.
13. J. Lin and R. G. Parker 2000 Journal of Sound and Vibration 233(5), 921-928. Structured vibration characteristics of planetary gears with unequally spaced planets.
14. D. L. Seager 1975 Journal of Mechanical Engineering Science 17, 293-298. Conditions for the neutralization of excitation by the teeth in epicyclic gearing.
15. A. Kahraman and G. W. Blankenship 1994 Proc. of International Gearing Conference, Newcastle, UK, 99-104. Planet mesh phasing in epicyclic gear sets.
16. A. Kahraman 1994 Journal of Mechanical Design 116(3), 713-720. Planetary gear train dynamics.
17. R. G. Parker 2000 Journal of Sound and Vibration 236(4), 561-573. A physical explanation for the effectiveness of planet phasing to suppress planetary gear vibration.
18. R. Kasuba and J. W. Evans 1981 Journal of Mechanical Design 103, 398-409. An extended model for determining dynamic loads in spur gearing.
19. A. Kahraman and G. W. Blankenship 1996 Journal of Sound and Vibration 194(3), 317-336. Interactions between commensurate parametric and forcing excitations in a system with clearance.
20. A. Kahraman and G. W. Blankenship 1997 Journal of Applied Mechanics 64, 217-226. Experiments on nonlinear dynamic behavior of an oscillator with clearance and periodically time-varying parameters.
21. J. Lin and R. G. Parker 2002 Journal of Sound and Vibration 249, 129-145. Planetary gear parametric instability caused by mesh stiffness variation.

Acknowledgment

The authors would like to thank Timothy L. Krantz of the Army Research Lab at NASA Glenn Research Center for his support and advice on the project. This material is based upon work supported by the U.S. Army Research Office under grant DAAD19-99-1-0218.