This paper presents the structured vibration mode and natural frequency properties of compound planetary gears of general description, including those with equally-spaced planets and diametrically opposed planet pairs. The vibration modes are classified into rotational, translational, and planet modes and the unique properties of each type are examined and proved for general compound planetary gears. All vibration modes fall into one of these three categories.
Introduction
Planetary gears are widely used in many applications due to advantages over parallel shaft arrangements such as high power density and large reduction in a small volume [1]. In fixed-ratio applications requiring a reduction of approximately 10:1 or less, a simple (i.e., single planet for each load path), single-stage planetary gear is often sufficient. For fixed-ratio applications requiring greater reductions, however, compound planetary gears are common. Automatic transmissions require more kinematic combinations than a single planetary can provide, so they also utilize compound planetary gears. Despite their benefits, compound planetary gears often have more noise and vibration problems than simple planetary gears.

Although the vibration of simple, single-stage planetary gears has been studied by many researchers (e.g., [4]- [16]), the vibration of compound or multi-stage planetary gearsets has received little research attention. Kiracofe and Parker [2] conducted a mathematical examination of the structured modal properties of planetary gears of very general description. Kahraman [3] considered a more limited study of the vibration of compound planetary gears. In that work, a purely rotational model that does not include gear translation is applied to a restricted class of compound planetary gears, and modal properties are given based on simulation rather than derivation.
For simple, single-stage planetaries, Lin and Parker [4] analyzed the free vibration and proved that there are exactly three types of modes: rotational, translational, and planet. They showed certain unique properties for these modes. These findings are consistent with finite element results [8]. Recent industry-motivated analyses by the authors investigated a variety of compound and multi-stage planetary gearsets and found that they all exhibited modal characteristics similar to a simple, single-stage planetary gear. The intent of this work is to generalize prior results and mathematically prove that compound, multi-stage planetary gear systems of general description possess highly structured modal properties analogous to simple, single-stage planetary gears.

Modeling and Equations of Motion
There are many different kinds of gearsets that are referred to as compound planetary gears. The present work attempts to be as general as possible in its definition. Three different types of compound planetary gears are described. The first two are the stepped planet planetary (Figure 1), and the meshed planet planetary (Figure 2) [17]. The third type, the multi-stage planetary, (Figure 3) is created by joining multiple planetary stages together, where each stage can be a simple, meshed, or stepped planetary. No limitations are imposed on which elements are the input or output members.
In deriving the equations of motion, it is necessary to systematically enumerate the three types of elements in a planetary gear: carriers, central gears (suns and rings), and planets. Let the carriers be numbered 1,2,…,a and the central gears be numbered 1,2,…,b. In order to describe the planets, it is convenient to divide them into groups.
First, each planet is always associated with one and only one carrier. Thus, it is natural to define a planet set to be all of the planets associated with a particular carrier. Within each planet set, the planets are partitioned into isolated planet trains. Two planets are considered to be in the same planet train if they: a) mesh with each other, or b) are connected to each other by a shaft (as in stepped planets). The planet train concept is illustrated in Figures 1 and 2.
Let the planet sets be numbered 1,2,…,a, where planet set i is associated with carrier i. Let the planet trains be numbered 1,2,…,![]() , where
, where ![]() designates the number of planet trains in planet set i. Let the planets in a train be numbered 1,2,…,
designates the number of planet trains in planet set i. Let the planets in a train be numbered 1,2,…,![]() , where designates the number of planets per planet train in planet set i. The model requires all planet trains in a planet set to have the same number of planets, which is generally the case in practical systems.
, where designates the number of planets per planet train in planet set i. The model requires all planet trains in a planet set to have the same number of planets, which is generally the case in practical systems.
A planar problem is considered where each carrier, planet, and central gear has three degrees of freedom: two translational and one rotational. The model has 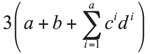 degrees of freedom.
degrees of freedom.
Translational![]() coordinates are assigned to the carriers and translational coordinates
coordinates are assigned to the carriers and translational coordinates![]() are assigned to the central gears (suns and rings). The
are assigned to the central gears (suns and rings). The ![]() and
and ![]() coordinates are positive towards the equilibrium position of the arbitrarily chosen first planet of the first planet train of the first planet set at time t=0. Translational coordinates
coordinates are positive towards the equilibrium position of the arbitrarily chosen first planet of the first planet train of the first planet set at time t=0. Translational coordinates![]() are assigned to planet m in planet train l in planet set i. These are radial and tangential coordinates.
are assigned to planet m in planet train l in planet set i. These are radial and tangential coordinates.

The equations of motion of a central gear are discussed as an example. The forces/moments on a central gear fall into five categories: gear-gear forces/moments, gear-carrier forces/moments, gear-ground bearing forces/moments, gear-planet mesh forces, and externally applied forces/moments. The first three are easily described. Modeling the interaction as a linear spring, such as from a connecting shaft, the gear-gear force between gears j and n in the x direction is described by![]() . Similar terms occur for the y and coordinates as well as the gear-carrier and gear-ground forces/moments. Note that central gears never mesh with other central gears. Gear-planet mesh forces are more described in [2].
. Similar terms occur for the y and coordinates as well as the gear-carrier and gear-ground forces/moments. Note that central gears never mesh with other central gears. Gear-planet mesh forces are more described in [2].
The equations of motion for the planets, central gears, and carriers are given in [2]. The equations of motion for the full system are written in matrix form as
![]() (1)
(1)

Natural Frequencies and Vibration Modes
To determine the natural frequencies and vibration modes the time-invariant system is considered. All mesh stiffnesses are considered to be constant and equal to their average stiffness over one mesh cycle. All externally applied forces/moments are assumed to be zero.
The associated eigenvalue problem derived from![]() is
is
![]() (2)
(2)
![]() (3)
(3)
The individual vectors for the carriers and gears are
![]() (4)
(4)
The planet set, planet train, and planet vectors are
![]() (5)
(5)
Expanding (2) into three groups of equations for the individual components according to the matrix definitions yields
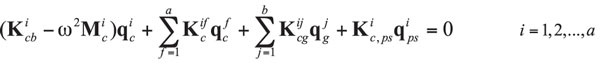 (6)
(6)
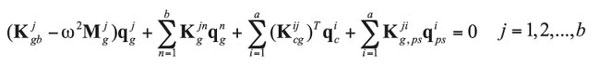 (7)
(7)
 (8)
(8)
The following additional assumptions are imposed:
1. All planet trains within a planet set are identical in all ways (mass, tooth parameters, bearing properties, etc.).
2. All planet trains are equally spaced around their associated carrier. The case with diametrically opposed pairs of planet trains is discussed later.
3. For each planet set i,![]() In practice, almost all planetary gears have three or more planets to take advantage of load sharing. The case with two equally spaced planet trains is considered later as a case of diametrically opposed planet trains.
In practice, almost all planetary gears have three or more planets to take advantage of load sharing. The case with two equally spaced planet trains is considered later as a case of diametrically opposed planet trains.
4. All bearing and shaft stiffnesses are isotropic.

The distinctive vibration properties are first illustrated by an example using the parameters in Table 1. This system is shown schematically in Figure 4. It is a two stage system where the first stage has both meshed and stepped planets and the second stage has only simple planets. The ring gear is common to both stages. The system has 66 degrees of freedom. The natural frequencies and their multiplicities are shown in Table 2.
All vibration modes for this system can be classified into one of three types. Typical vibration modes of each type are shown in Figure 5, Figure 6, Figure 7. The equilibrium positions of the gears and carriers are shown as dashed lines. The equilibrium positions of the planets with respect to the displaced carriers are shown as light lines. The displaced positions of the suns and planets are shown as heavy lines. Dots represent the component centers. Motion of the ring is omitted for clarity.

Figure 5 illustrates a type of mode where all central gears and carriers have pure rotation and no translation. These are named rotational modes. In a rotational mode, all planet trains within a given planet set have identical motion. There are exactly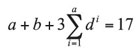 rotational modes, each with an associated natural frequency of multiplicity one (distinct).
rotational modes, each with an associated natural frequency of multiplicity one (distinct).
Figure 6 shows a pair of degenerate modes that have the same natural frequency. All central gears and carriers have pure translational motion with no rotation. These are called translational modes. There are exactly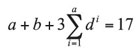 degenerate pairs of translational modes, where each pair has an associated natural frequency of multiplicity two. Well-defined relations between the planet motions will be shown.
degenerate pairs of translational modes, where each pair has an associated natural frequency of multiplicity two. Well-defined relations between the planet motions will be shown.


Figure 7 illustrates two modes where the carriers and central gears have no motion; the planets are the only components that deflect. These are called planet modes. A given mode is associated with motion of the planets of exactly one planet set and planets in all other planet sets have no motion. In general, each natural frequency associated with planet set i has multiplicity![]() Thus, planet modes exist only for planet sets containing four or more planet trains. If planet modes exist for planet set i, then there are
Thus, planet modes exist only for planet sets containing four or more planet trains. If planet modes exist for planet set i, then there are ![]() different natural frequencies for that set’s planet modes (each with multiplicity
different natural frequencies for that set’s planet modes (each with multiplicity![]() So, there are exactly planet modes.The number of different natural frequencies for a planet set’s planet modes is dictated by the number of degrees of freedom in one planet train; their multiplicity is dictated by the number of trains in the set. Finally, each planet train’s motions are a scalar multiple of the first (or any arbitrarily chosen) planet train’s motions. Equations governing these scalars will be derived.
So, there are exactly planet modes.The number of different natural frequencies for a planet set’s planet modes is dictated by the number of degrees of freedom in one planet train; their multiplicity is dictated by the number of trains in the set. Finally, each planet train’s motions are a scalar multiple of the first (or any arbitrarily chosen) planet train’s motions. Equations governing these scalars will be derived.

The above properties of the modes, which have been drawn from numerical results, can be proven analytically [2]. The proof proceeds by proposing candidate modes based on the numerical results and substituting them into the equations of motion. For each type of mode, a reduced degree of freedom eigenvalue problem is found. The total number of eigenvalues is shown to equal the total number of degrees of freedom in the system, so the three mode types are an exhaustive list of the possible mode types.
Rotational Modes
A rotational mode has the form (3) – (5) simplified as
 (9)
(9)
Algebraic reductions of (6) – (8) yield an order reduced eigenvalue problem involving the non-zero degrees of freedom in (9). Its solution gives![]() natural frequencies and rotational modes.
natural frequencies and rotational modes.

From the solutions of the reduced eigenvalue problem, rotational vibration modes of the full system are constructed according to (9). These eigenvalues are distinct, in general.
Translational Modes
A pair of translational modes of the form (3) – (5) with degenerate natural frequency is given by
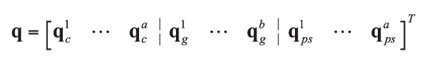 (10)
(10)
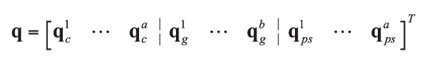 (11)
(11)
These are orthogonal with respect to the mass matrix such that![]() . The carrier, gear, and planet translations are related by1
. The carrier, gear, and planet translations are related by1
![]() (12)
(12)
 (13)
(13)
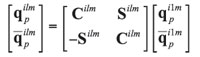 (14)
(14)
where![]() , and I is the 3×3 identity matrix. It remains to show that this candidate mode pair satisfies (6) – (8), and this is presented in detail in [2]. Thus, if all planet sets have three or more planet trains, then there are
, and I is the 3×3 identity matrix. It remains to show that this candidate mode pair satisfies (6) – (8), and this is presented in detail in [2]. Thus, if all planet sets have three or more planet trains, then there are![]() numerically different translational natural frequencies, each with multiplicity two.
numerically different translational natural frequencies, each with multiplicity two.
Planet Modes
A planet mode associated with planet set i is written in the form
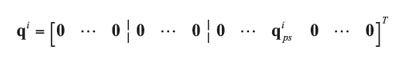 (15)
(15)
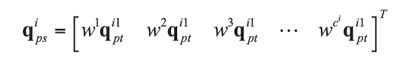 (16)
(16)
with ![]() defined in (5) and
defined in (5) and![]() denoting a particular planet set. Insertion of (15) – (16) into (6) – (8), expansion using matrix definitions, and use of algebraic reductions similar to those for rotational and translational modes yields the reduced order eigenvalue problem for the motion of a single planet train
denoting a particular planet set. Insertion of (15) – (16) into (6) – (8), expansion using matrix definitions, and use of algebraic reductions similar to those for rotational and translational modes yields the reduced order eigenvalue problem for the motion of a single planet train
![]() (17)
(17)
There are![]() eigensolutions of the reduced problem (17). The eigenvalues are distinct, in general.
eigensolutions of the reduced problem (17). The eigenvalues are distinct, in general.
It remains to determine the![]() in (16). Examination of the forces acting on the system for deflection in a planet mode yield three constraints on the
in (16). Examination of the forces acting on the system for deflection in a planet mode yield three constraints on the![]() [2]
[2]
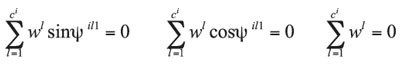 (18)
(18)
Ambarisha and Parker [9] proved that for a simple planetary gear the number of independent solutions of (18) is exactly![]() . Thus, planet modes exist only for planet sets with four or more planet trains. Wu and Parker [7] give the following
. Thus, planet modes exist only for planet sets with four or more planet trains. Wu and Parker [7] give the following![]() closed-form, independent solutions based on their consideration of simple planetary gears
closed-form, independent solutions based on their consideration of simple planetary gears
 (19)
(19)
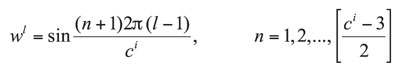 (20)
(20)
where the brackets in (19) and (20) denote the ceiling and floor functions, respectively.
For each eigensolution of the reduced problem (17),![]() independent vibration modes of the full problem (1), each having the same natural frequency, are constructed from (15), (16), and the
independent vibration modes of the full problem (1), each having the same natural frequency, are constructed from (15), (16), and the![]() independent solutions of (18). Thus, for each planet set
independent solutions of (18). Thus, for each planet set![]() there are
there are![]() vibration modes of the form (15)-(16); these are grouped into
vibration modes of the form (15)-(16); these are grouped into![]() sets of degenerate modes, where each set has an associated natural frequency of multiplicity
sets of degenerate modes, where each set has an associated natural frequency of multiplicity ![]()
Diametrically Opposed Planet Positions
In certain situations, assembly constraints cause the planet trains to be unequally spaced around the carrier. In the general case, this causes the rotational and translational modes to couple and lose their distinctive properties. One special case of interest is the diametrically opposed case in which pairs of planets trains are 180 deg apart. In other words, for some![]() is even, and
is even, and![]() . This is common in practice. Each pair may be arbitrarily spaced.
. This is common in practice. Each pair may be arbitrarily spaced. ![]() is allowed, which is an exception to assumption 3. For
is allowed, which is an exception to assumption 3. For ![]() , the terms “equally spaced” and “diametrically opposed” are equivalent. The properties of such a planet set follow the results for the diametrically opposed case.Lin and Parker considered diametrically opposed planets for a simple, single stage planetary gears in [12].
, the terms “equally spaced” and “diametrically opposed” are equivalent. The properties of such a planet set follow the results for the diametrically opposed case.Lin and Parker considered diametrically opposed planets for a simple, single stage planetary gears in [12].
The rotational and planet modes retain their properties in the diametrically opposed case. The translational modes, however, are modified for the diametrically opposed case. Specifically, translational modes have distinct eigenvalues instead of multiplicity two, but they retain their modal character of the suns, rings, and carriers having only translation and no rotation.
Discussion
While the mathematical proof is of interest mainly to the academic researcher, the results are useful for both the practical gearbox designer and the academic researcher. To a gearbox designer, the prediction of natural frequencies allows resonance conditions to be avoided when designing a planetary gear system. The classification of modes into various types and knowledge of the number of numerically different natural frequencies is also important for avoiding resonant response, reducing excitation of particular mode types, and understanding whether response in a particular mode will generate torque (rotational modes), force (translational modes) or neither (planet modes) to the structures supporting the central gears (sun and ring). In cases where design constraints require operating tooth mesh frequencies to be near natural frequencies, the use of planet mesh phasing can suppress resonant response [9], [14], [18], [19]. Understanding and application of planet mesh phasing depends on the unique properties of planetary gear free vibration as shown here. Future work on understanding the various mode types may identify certain types of modes as having more significant impact on noise, fatigue life, and other factors of interest.
For research purposes, extension of the dynamic model of simple planetary gears to the general compound case allows other investigations of simple planetary gear vibration to be extended to the compound case. Research on nonlinear response, parametric excitation from fluctuating mesh stiffness, elastic ring deformation, etc. (e.g.,[7], [8], [10], [20], [21], [22]) can be carried out for general compound planetary gears. These analyses benefit from understanding the properties of the different mode types, particularly because such analyses frequently adopt the assumption that only one or two modes are present in the response (modal truncation). In that case, one can examine the interactions between two modes of the same or different types. For example, is a combination parametric instability possible between a rotational and translational mode?
Summary and Conclusions
For identical, equally spaced planet trains, the natural frequencies and vibration modes of compound planetary gears have highly structured properties due to the system’s cyclic symmetry. Specifically, all vibration modes can be classified into one of three types: rotational, translational, and planet modes. Rotational modes with distinct natural frequencies have pure rotation of the central gears and all planet trains in a given planet set move identically. Pairs of translational modes with degenerate natural frequencies have pure translation of the carriers and central gears, and motions of the planet trains in a pair of orthonormal vibration modes can be found by a simple transformation of the first planet train’s motion. Planet modes have motion of the planets in one planet set only and no motion of any carriers or central gears; the multiplicity of their natural frequencies is dictated by the number of planet trains in a planet set. Reduced order eigenvalue problems for each mode type are given explicitly.
References
1. Smith, J. D., 1983, Gears and Their Vibration: A Basic Approach to Understanding Gear Noise.
2. Kiracofe, D. R. and Parker, R. G.., 2007, “Structured Vibration Modes of General Compound Planetary Gear Systems”, ASME Journal of Vibration and Acoustics. 129, pp. 1-16.
3. Kahraman, A., 2001, “Free Torsional Vibration Characteristics of Compound Planetary Gear Sets”, Mechanism and Machine Theory. 36, pp. 953-971.
4. Lin, J. and Parker, R. G., 1999, “Analytical Characterization of the Unique Properties of Planetary Gear Free Vibration”, Journal of Vibration and Acoustics. 121, pp. 316 ? 321.
5. Sun, T. and Hu, H. Y., 2003, “Nonlinear Dynamics of a Planetary Gear System with Multiple Clearances”, Mechanism and Machine Theory. 38, pp. 1371-1390.
6. Saada, A. and Velex, P., 1995, “An Extended Model for the Analysis of the Dynamic Behavior of Planetary Trains”, ASME Journal of Mechanical Design 117, pp. 241-247.
7. Wu, X. and Parker, R. G., 2007, “Modal Properties of Planetary Gears with an Elastic Continuum Ring Gear”,.ASME Journal of Applied Mechanics. In press.
8. Parker, R. G., Agashe, V. and Vijayakar, S. M., 2000, “Dynamic Response of a Planetary Gear System Using a Finite Element/Contact Mechanics Model”, Journal of Mechanical Design, 122, pp. 305-311.
9. Ambarisha, V. K. and Parker, R.G., 2006, “Suppression of Planet Mode Response in Planetary Gear Dynamics through Mesh Phasing”, Journal of Vibration and Acoustics. 128, pp. 133-142
10. Ambarisha, V. K. and Parker, R. G., 2006, “Nonlinear Dynamics of Planetary Gears using Analytical and Finite Element Models”, Journal of Sound and Vibration. 302, pp. 577-595.
11. Kahraman, A., 1994, “Natural Modes of Planetary Gear Trains”, Journal of Sound and Vibration. 173 (1) pp. 125-130.
12. Lin, J. and Parker, R. G., 2000, “Structured Vibration Characteristics of Planetary Gears with Unequally Spaced Planets”, Journal of Sound and Vibration. 233 (5) pp. 921-928.
13. Lin, J. and Parker, R. G., 2001, “Natural Frequency Veering in Planetary Gears”, Mechanics of Structures and Machines. 29 (4), pp. 411- 429.
14. Parker, R. G., 2000, “A Physical Explanation for the Effectiveness of Planet Phasing to Suppress Planetary Gear Vibration”, Journal of Sound and Vibration. 236 (4) pp. 561-573.
15. Lin, J. and Parker, R. G., 1999, “Sensitivity of Planetary Gear Natural Frequencies and Vibration Modes to Model Parameters”, Journal of Sound and Vibration, 228 (1), pp. 109-128.
16. Cunliffe, F., Smith, J. D. and Welbourn, D. B., 1974, “Dynamic Tooth Loads in Epicyclic Gears”, Journal of Engineering for Industry, 96 (2), pp. 578-584.
17. M~{(9~}ller, H. W., 1982, Epicyclic Drive Trains: Analysis, Synthesis, and Applications. Translated from German by Manhardt, W. G.
18. Seager, D. L., 1975, “Conditions for the Neutralization of Excitation by the Teeth in Epicyclic Gearing”, Journal of Mechanical Engineering Science. 17 (5), pp. 293-298.
19. Kahraman, A. and Blankenship, G. W., 1994, “Planet Mesh Phasing in Epicyclic Gear Sets” Proceedings of International Gearing Conference, Newcastle, UK, pp. 99-104.
20. Kahraman, A., Kharazi, A. A., and Umrani, M., 2003, “A Deformable Body Dynamic Analysis of Planetary Gears with Thin Rims”, Journal of Sound and Vibration. 262, pp. 752-768.
21. Lin, J. and Parker, R. G., 2002, “Planetary Gear Parametric Instability Caused by Mesh Stiffness Variation”, Journal of Sound and Vibration. 249 (1), pp. 129-145.
22. Velex, P. and Flamand, P., 1996, “Dynamic Response of Planetary Trains to Mesh Parametric Excitations”, Journal of Mechanical Design. 118, pp. 7-14.





































